一般進化論

general theory of evolution

general theory of evolution
(注) 不慣れな言葉が出てきますが、あとでわかるようになりますので気にしないで読み進めてください。
世界のあらゆる物的存在(物理的に表現された情報を含む)は、散逸構造(さんいつこうぞう)です。
散逸(さんいつ)とは、整理されてまとまっていた書物や文献などが、バラバラに散って乱雑な状態になり、何がどこにあるのかわからなくなってしまうことです。
世の中のあらゆるものは、そういう散逸構造であり、「整理してひとまとめにしておく努力」が失われると、バラバラになっていきます。

人体は散逸構造(さんいつこうぞう)です。毎日食べて、ウンチをして、生きる努力をしなければ死んでバラバラになってしまいます。
国家は散逸構造です。たくさんの人間が協力し合ってまとまり国体を維持する努力を怠るようになれば、国家は崩壊してバラバラになります。
世界は、いろいろな散逸構造が集まってできています。
ダーウィンの生物進化論は、すべての散逸構造に適用できます。
ダーウィンの進化論は「生物対象の特殊進化論」なので、適用を散逸構造全体に拡大したものは「一般進化論」ということになります。
つまり、私たちホモサピエンスが知覚でとらえている世界の森羅万象は、「様々な散逸構造の進化の過程」であると理解することができます。
環境変化にうまく適応できている散逸構造は長く生き残り、うまく適応できなくなった散逸構造は壊れて消え去ります。
科学の用語で説明を受けると少し難しそうに思えるかもしれませんが、このような理解の仕方は仏教の世界観そのものなので、多くの日本人にとって難しい話ではありません。
仏教の世界観を知らない西洋人などは、小難しい自然科学の言葉を使わないと理解が難しいのでしょう。
このウェブページでは、仏教の世界観を知っている日本人を対象として、なるべくわかりやすく一般進化論を紹介します。
生物は散逸構造(さんいつこうぞう)であり、生物についてのダーウィンの進化論はすべての散逸構造に適用できます。
生物以外にも拡大した進化論を「一般進化論」と私は呼んでいます。
一般進化論は、実は仏教のエッセンスそのものであり、日本人にはとても馴染みのある考え方です。
「平家物語」の世界観は、仏教の無常観です。
祇園精舎の鐘の声、諸行無常の響あり。娑羅双樹の花の色、 盛者必衰の理を顕はす。奢れる人も久しからず。唯春の夜の夢のごとし。猛き者も遂にはほろびぬ、偏に風の前の塵に同じ。
ぎおんしょうじゃのかねのこえ、しょぎょうむじょうのひびきあり。さらそうじゅのはなのいろ、じょうしゃひっすいのことわりをあらわす。おごれるひともひさしからず、ただはるのよのゆめのごとし。たけきものもついにはほろびぬ、ひとえにかぜのまえのちりにおなじ。
参考解説:【全文ふりがな付き】平家物語冒頭「祇園精舎の鐘の声」の意味を徹底解説!(2024.08.20):▶ ▶ ▶
鴨長明の「方丈記」で描かれているのも散逸構造(さんいつこうぞう)です。
ゆく河の流れは絶えずして、しかも、もとの水にあらず。淀みに浮ぶ泡沫(うたかた)は、かつ消え、かつ結びて、久しくとどまりたる例(ためし)なし。世の中にある、人と栖(すみか)と、又かくのごとし。
たましきの都のうちに、棟(むね)を並べ、甍(いらか)を争へる、高き、いやしき人の住ひは、世々(よよ)を経て、尽きせぬ物なれど、是(これ)をまことかと尋(たずぬ)れば、昔しありし家は稀なり。或は去年(こぞ)焼けて今年つくれり。或(あるい)は大家(おほいえ)ほろびて小家(こいへ)となる。住む人も是に同じ。所もかはらず、人も多かれど、いにしへ見し人は、二三十人が中に、わづかにひとりふたりなり。朝(あした)に死に、夕(ゆふべ)に生るるならひ、ただ水の泡にぞ似りける。
不知(しらず)、生れ死ぬる人、何方(いづかた)より来たりて、何方へか去る。また不知、仮の宿り(やどり)、誰が為(たがため)にか心を悩まし、何によりてか目を喜ばしむる。その、主(あるじ)と栖(すみか)と、無常を争ふさま、いはばあさがほの露に異ならず。或(あるい)は露落ちて花残れり。残るといへども、朝日に枯れぬ。或は花しぼみて露なほ消えず。消えずといへども、夕(ゆふべ)を待つ事なし。
参考解説:鴨長明の方丈記|無常観とは?内容解説|原文と現代語訳(2020.02.28):▶ ▶ ▶
参考解説:【全文】鴨長明『方丈記』原文と現代語訳をわかりやすく解説(2024.04.21):▶ ▶ ▶
仏教の世界観を受容する文化的素地のない西洋人等は、「ダーウィンの生物進化論」や熱力学、「イリヤ・プリゴジンの散逸構造論」などで出てくるエネルギー、情報、エントロピー、熱力学第2法則といった科学的な用語を使った説明を通じてでないと「無常の世界観」を理解することが難しいのかもしれません。
そういうことから考えると、(中国や)日本には仏教伝来以前から似たような世界観があったのだろうと考えられます。
では、般若心経(はんにゃしんぎょう)の動画を2つ
最初の1分後に「色即是空 空即是色」が出てくるので、そこまで聴けばよいでしょう。
【作業用BGM (1hour) 】般若心経ミュージック動画 - 2020年総集編 - / 薬師寺寛邦 キッサコ(歌う僧侶 薬師寺寛邦 キッサコ / Kanho Yakushiji)(56:47)
【リラックス音楽 (30分間) 】般若心経ミュージック遍路 - 2022年前半【総集編】/ 薬師寺寛邦 キッサコ(歌う僧侶 薬師寺寛邦 キッサコ / Kanho Yakushiji)(31:48)
簡単に言うと、散逸構造(さんいつこうぞう)とは、川の流れの途中に生じる渦模様(うずもよう) のようなものです。
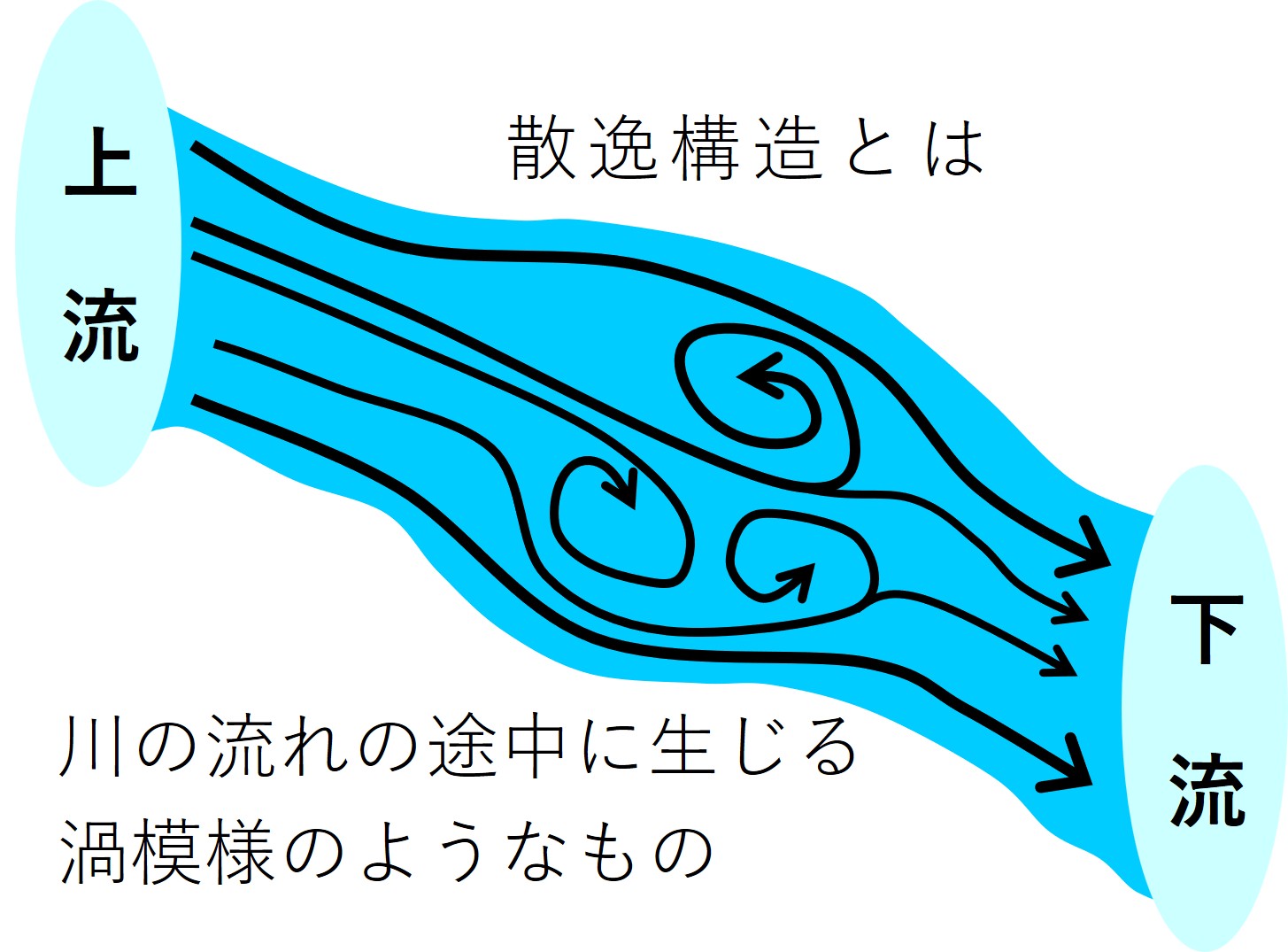
模様は別に渦巻でなくても構いません。何らかの水模様です。
そうした水模様を思い浮かべることができれば、次のことは容易に理解できると思います。
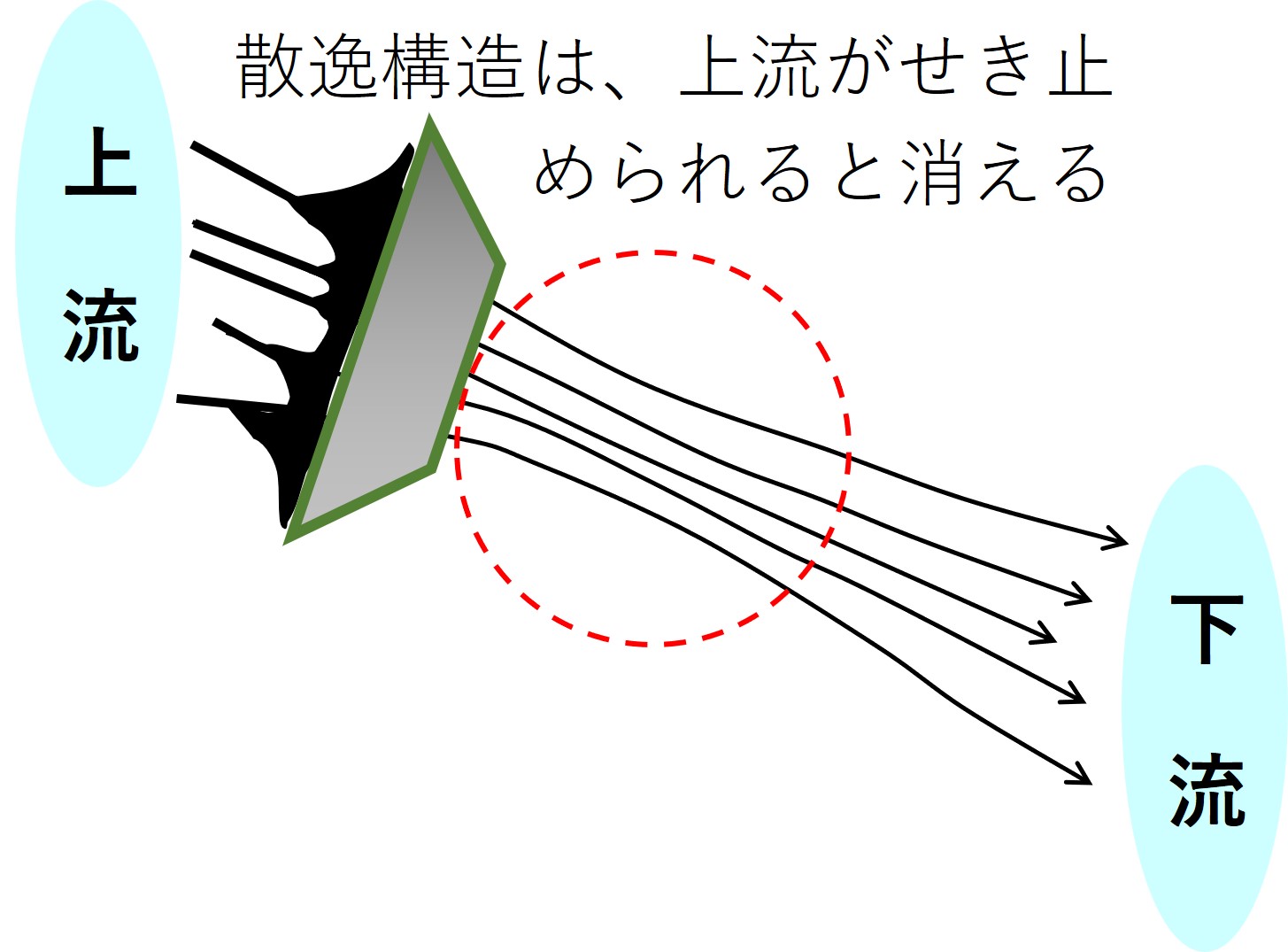
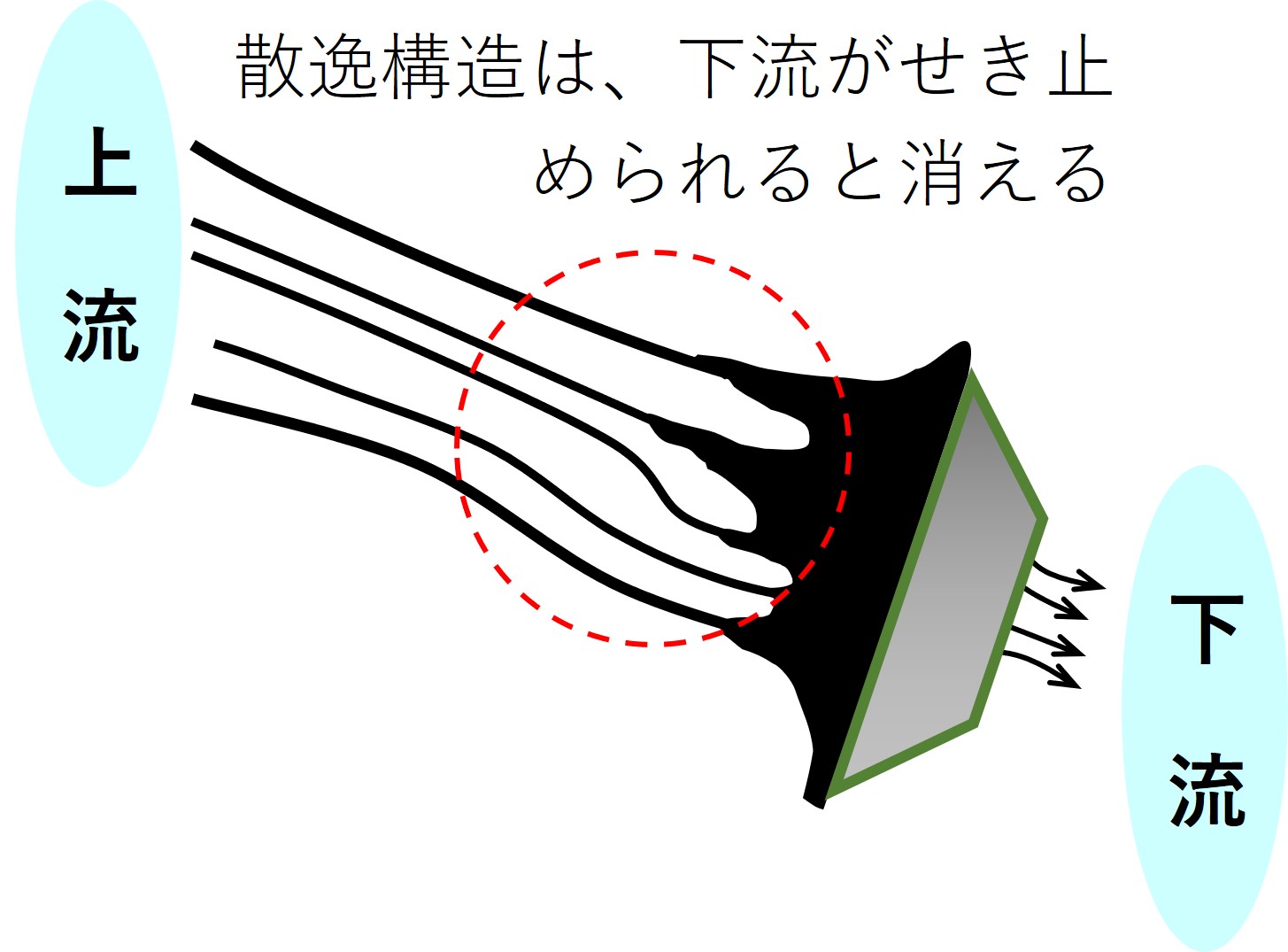
水模様に出入りする水の流れが妨げられると、最初にあった水模様は消えます。
模様は、あくまで水の流れの中で生じているのです。
では、水模様の中では何が起こっているのでしょうか?
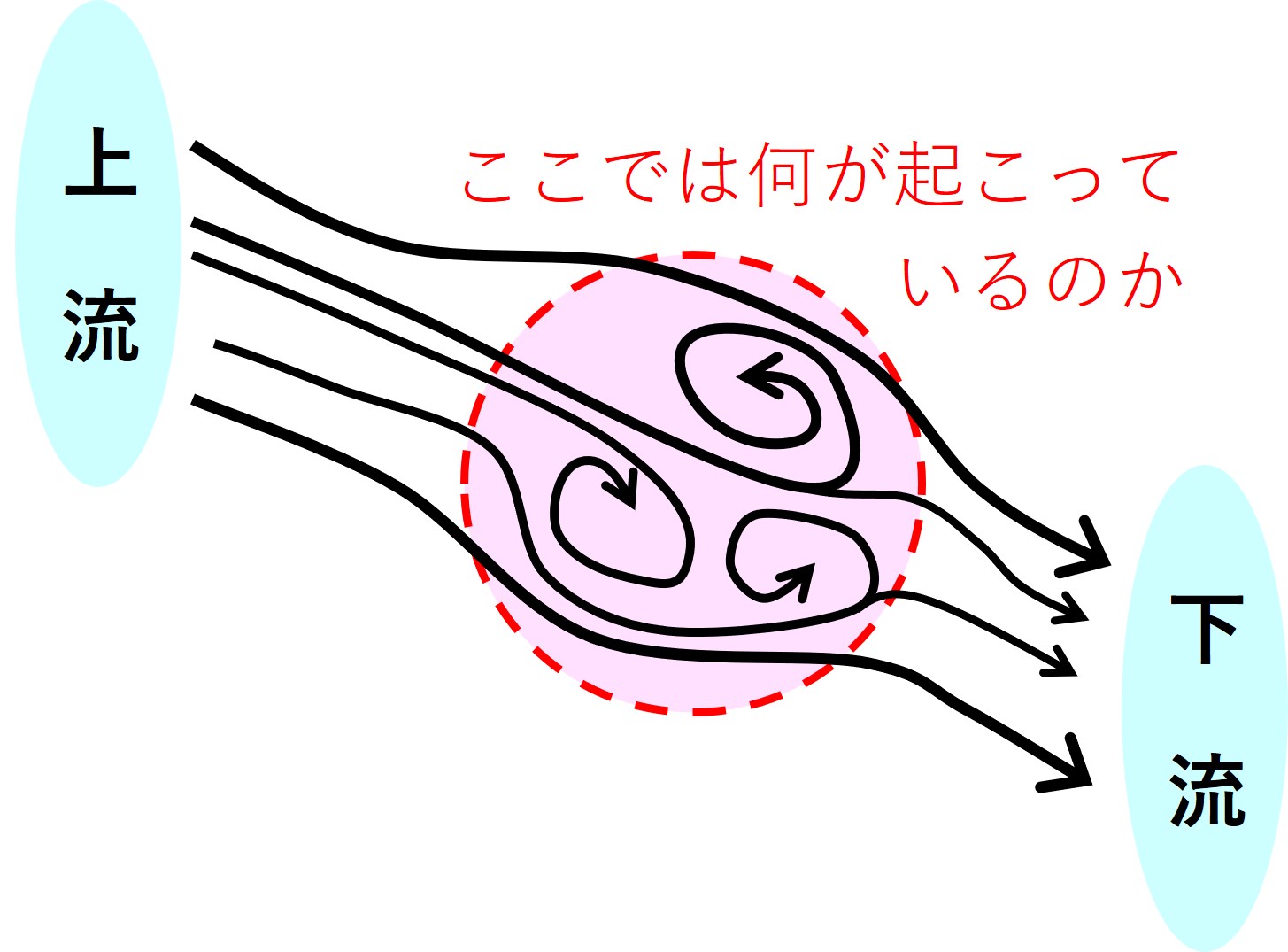
ここから先は、日本人には不要な「まわりくどい説明」となります。エントロピーが出てきますが、理解できなくても、な ~ん にも気にする必要はありません。日本人は日本文化を通じて本質を知っています。エントロピーが難しいときは 第8説明 へ飛ぶと良いでしょう。第8説明は主にエネルギーを使った説明になっています。
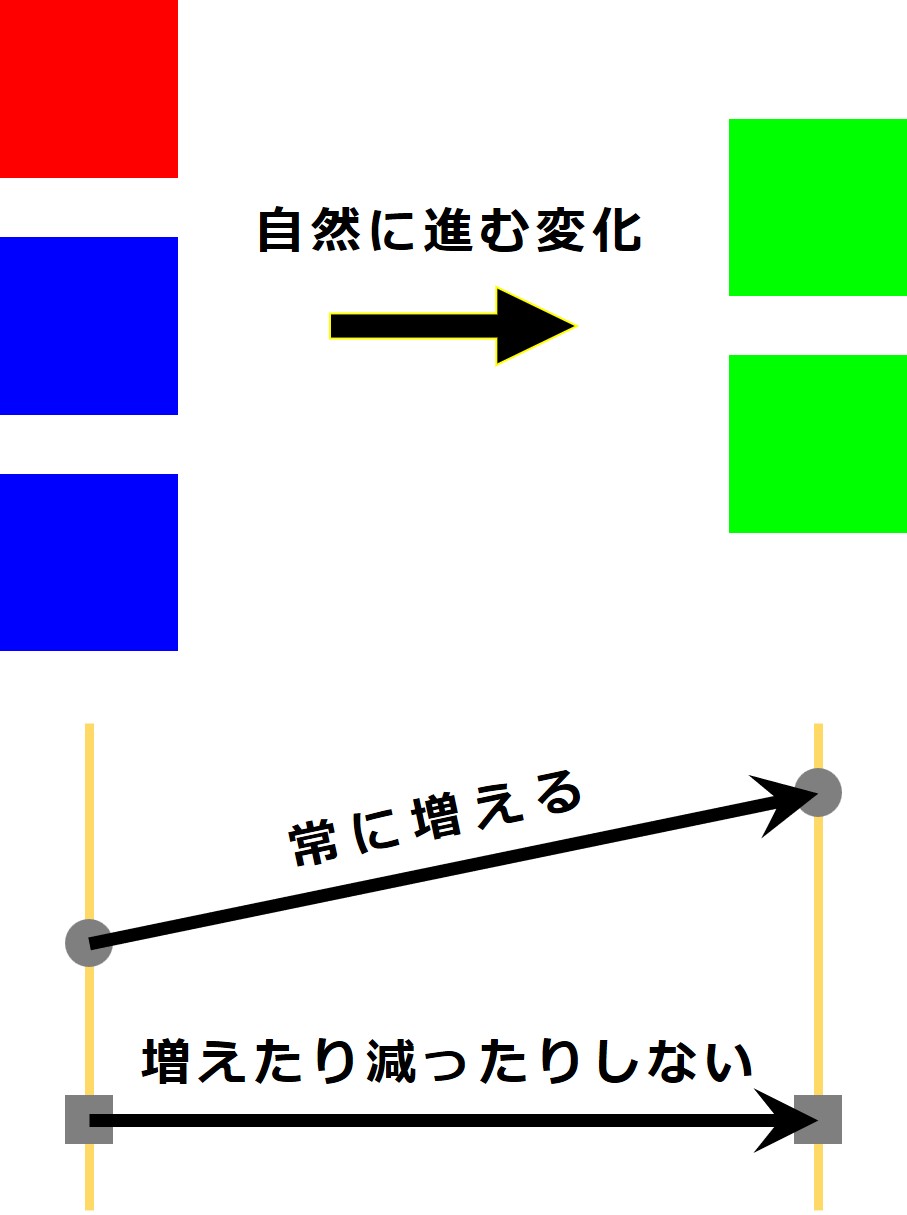
自然に進む物理的な変化や化学的な変化を観察していて、西洋の科学者は、「変化の前後で増えたり減ったりしないで常に保存される物理量」と「変化の前後で常に増える物理量」があることに気づきました。
科学者は前者をエネルギーと名付け、後者をエントロピーと名付けました。
では、まず エントロピー entropy について説明します。
エントロピーとは、「単位時間に現れている情報の総量」のことです。
次の図をご覧ください。
4枚のカードがあります。
それぞれのカードに絵のようなものがあります。
絵は静止しています。
カードの1枚1枚が、それぞれひとつの情報を表しています。
簡単な絵もあれば、複雑な絵もありますが、どれも情報としては「等価」です。

日常語では、複雑な絵に対して「情報量が多い」といった表現をしますが、そうした表現方法はここでは理解の邪魔(じゃま)になります。
日常語で情報量が多いとか少ないとか言っているときの情報は、「(情報の受け取り手に与えている)意味」のことです。
ひとつの情報が受け取り手に与える意味は、受け取り手によって異なります。
見た目が簡単だろうが、複雑だろうが、変化していない静止した構造は「ひとつの情報(=構造)」であると捉えます。
そして情報(=構造)とは、言い換えると「分布の偏り」のことです。
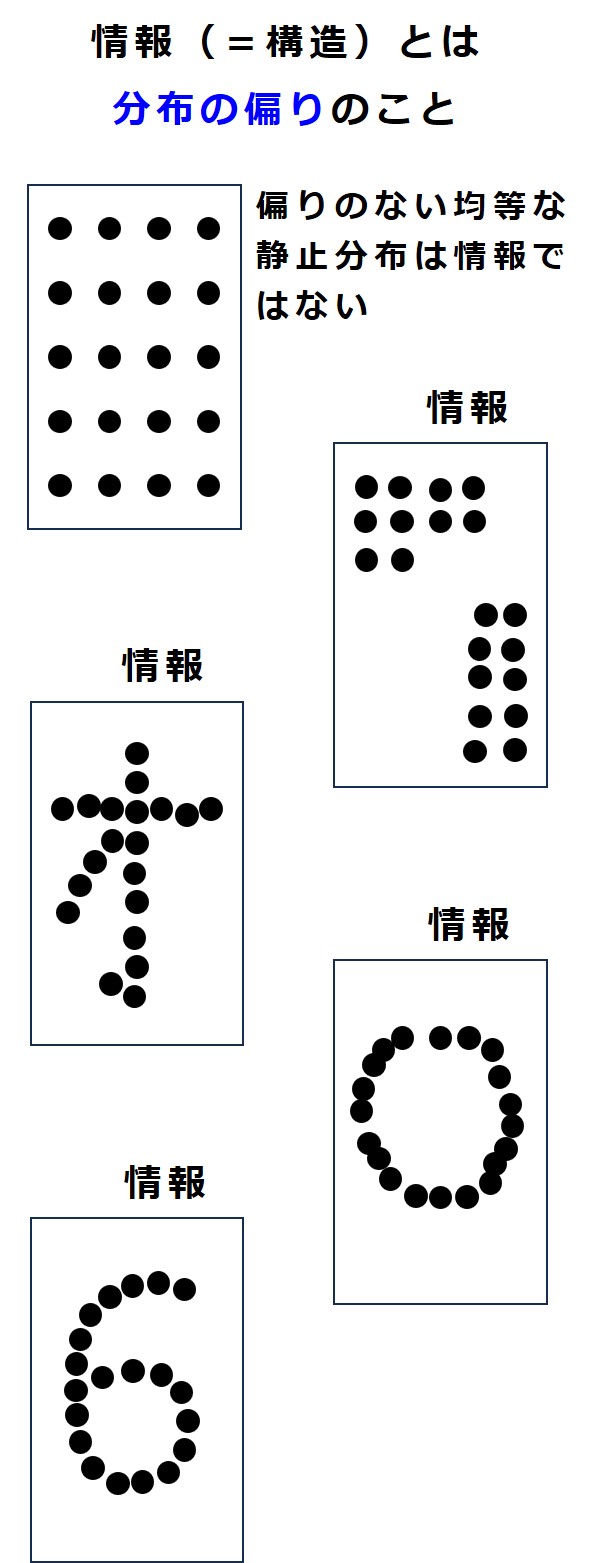
したがって、静止した絵のカード4枚全体をまとめて「ひとつの情報」と捉えることもできます。
そこで、宇宙規模で考えることにします。
そして、カエルの目で宇宙全体を見ることにします。
カエルの目?
カエルは動いているものしか見ていないそうです。
動いているものが小さければエサかも知れないと思って口の中に入れるようです。
まず「静止した宇宙」を扱います。
カエルの目で見ると、静止した宇宙全体が持つ情報としての価値は「ゼロ」です。
言い換えると、動いていないものがエサである可能性はカエルにとっては「ゼロ」です。
カエルはこの宇宙を飲み込もうとはしません。
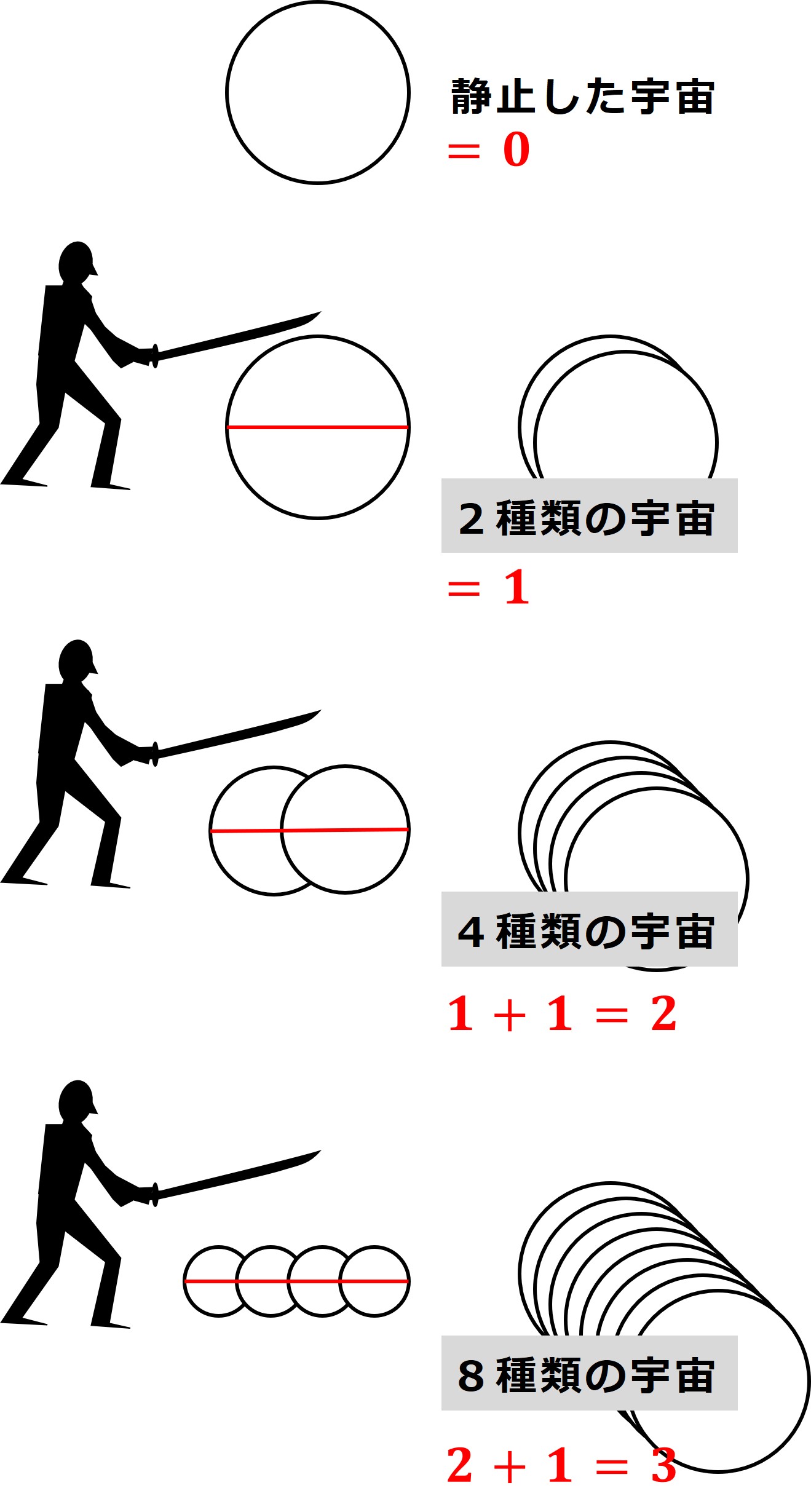
さて、ひとつの宇宙にサムライが近づき、真っ二つに切り裂いたとします。宇宙が2つになりました。
宇宙が2つになる動きがカエルの目には見えます。
カエルの目で見ると、分割された2種類の宇宙全体が持つ情報としての価値は「1」です。分割の動きが1回見えたということです。
(2枚のカードとは異なり)2つの宇宙はすぐに拡がり、重なり合います。
宇宙は2つに切り裂かれ、別々の宇宙ができたのに重なっているなんて、なんとなく量子力学っぽい素敵な世界です。
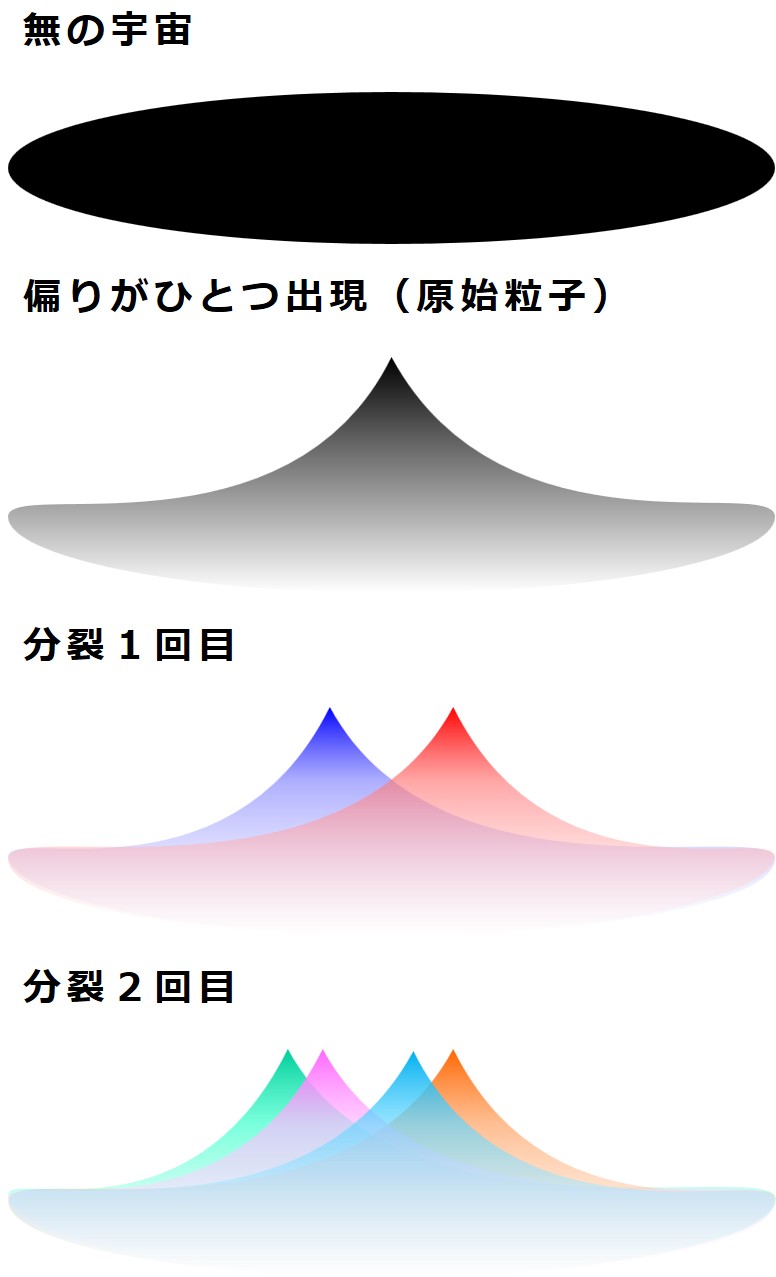
カエルは大きく口を開けて宇宙を飲み込んでも良いのですが、慎重な性格なのでもう少し様子を見ることにします。
そこにまたサムライが近づき、2種類の宇宙を真っ二つに切り裂いたとします。宇宙が4つになりました。
2つの宇宙が4つになる動きがカエルの目には見えます。
カエルの目で見ると、2分割を2回受けてできた4種類の宇宙全体が持つ情報としての価値は「2」です。
最初から数えると分割の動きが合計2回見えたということで、カエルは宇宙全体が自分のエサかもしれないという確信の度合いを強めていきます。
| 切断回数 | W:宇宙の種類 | Log2 W |
| 0 | 1 | 0 |
| 1 | 2 | 1 |
| 2 | 4 | 2 |
| 3 | 8 | 3 |
| 4 | 16 | 4 |
| 5 | 32 | 5 |
| 6 | 64 | 6 |
| 7 | 128 | 7 |
| 8 | 256 | 8 |
| 9 | 512 | 9 |
| 10 | 1024 | 10 |
| ~ | ~ | ~ |
| 666 | 3.06 ✕ 10 200 | 666 |
サムライが666回カタナを振り下ろし、宇宙全体の持つ情報の価値が「666」に到達した時、カエルは宇宙全体を間違いなくエサだと確信し、丸呑みしてしまいました。
以上、時計は無いけれど物事が順におこる世界で、カエルの目で宇宙全体を眺めて「情報の価値」が大きくなっていく様子を見ました。
このとき、宇宙の種類と「情報の価値」との対応は対数で換算可能です。
先の例だと、こんな感じです(↓)。
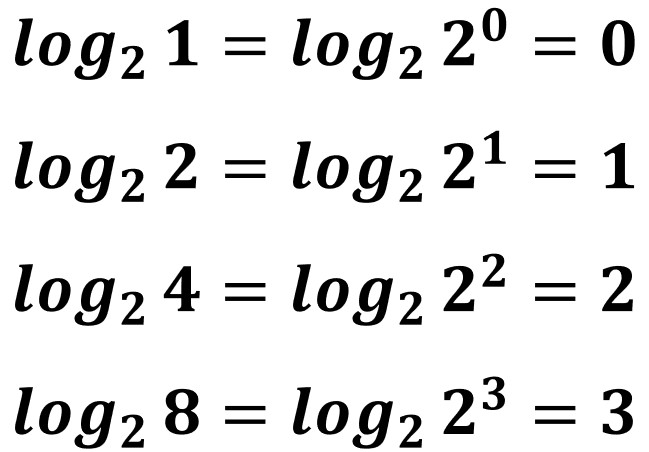
もちろん宇宙の種類の数をそのまま扱っても良いのですが、ホモサピエンスの脳のキャパシティーに合わせて扱う数を小さくするために、またわかりやすく「無価値=0」とするために、また将来エントロピーをわかりやすく足し算で扱うために、情報の価値の大きさには対数を使います。
指数とか、対数とか、はるか昔に忘れたという方は、次の簡単な計算例を見て少し思い出してください。
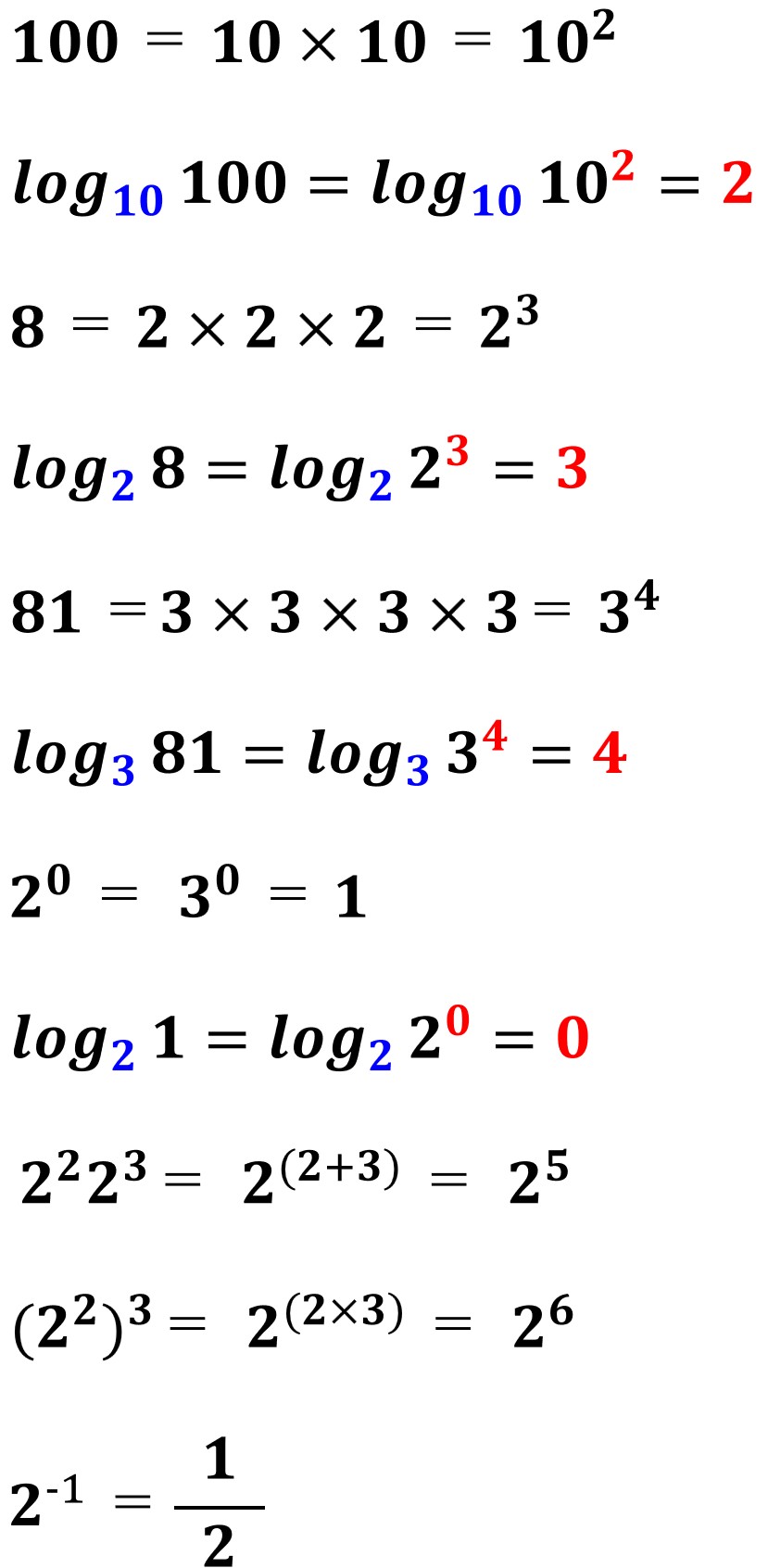
では次に、時計のある世界に戻り「情報の価値(希少価値)」を考えます。
ある所に悪魔がいて、6億円相当の宝の隠し場所を示す「A」と、ほぼ同じ6億円相当の宝の隠し場所を示す「B」と、2枚のカードを持っています。

悪魔に宝のありかを教えろと求めると、悪魔は2枚のカードのうち1枚を選んで見せてくれます。
このとき悪魔は、「A」を選んだときは3回、「B」を選んだときは1回見せます。

さて、大勢の貪欲な人々が集まり、悪魔に宝のありかを教えろと求めました。
悪魔の見せてくれる「A」と「B」のカードのどちらに価値があるでしょうか。
もちろん「B」ですね。
3回表示される「A」は読み取りやすいので、お宝に近づくライバルが増えます。
1回だけ表示される「B」を読み取ることができたときは、お宝を独占できるかもしれません。
悪魔が一定の確率で「A(確率:3/4)」か「B(確率:1/4)」を繰り返し選んで見せる時も情報の価値は同様です。
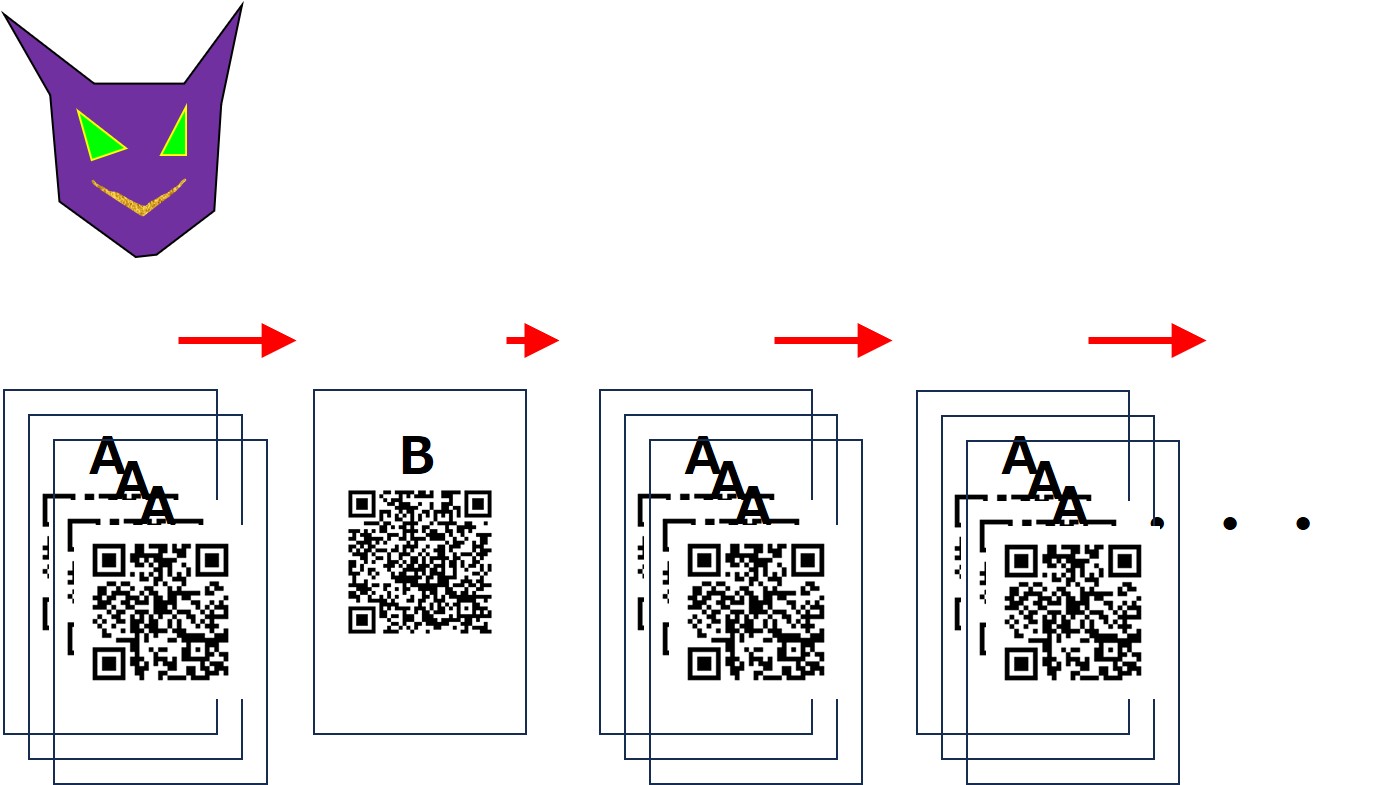
出現する確率が低いほどカードの価値は大きくなります。
日常では「確率的な 希少価値(きしょうかち)」と呼ばれています。
カード「A」も「B」も、6億円相当の宝のありかを示しているので、見せられる回数が少なくなればなるほど(出現確率が小さくなるほど)、情報としての希少価値は大きくなります。
そこでカード「 i 」の出現確率を Pi とし、確率が小さいほど計算値が大きくなるように逆数 1/Pi をとり、対数化して log(1/Pi)にしたものを考えます。ここで示す計算式は、考案可能な数式のひとつに過ぎません。
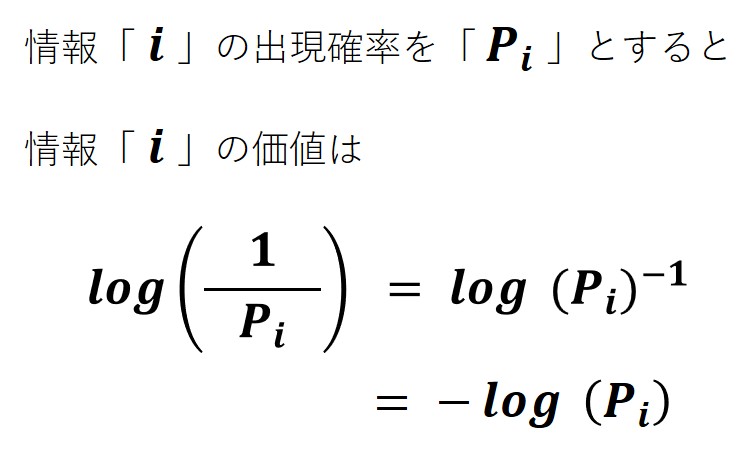
たとえば対数の底を 2 とすると、
カード「A(出現確率 3/4)」の希少価値は
log2(1/(3/4)) = 0.4150・・・
カード「B(出現確率 1/4)」の希少価値は
log2(1/(1/4)) = 2
と計算されます。
貧富の差が大きく見えます。
読まなくてよい注記:正統派の数学ではこの「情報の希少価値」を「情報量」と呼んでいますが、ここでは無視して、次に説明するものを「情報量」とします。
このとき、カード「A」などの出現確率は、単位時間当たりの出現回数や出現時間にも対応しています。
そこで、「出現確率 ✕ 情報の希少価値」を計算して「情報の量」とします。その計算式には確率が2回出てきて、まるで二重課税のような気持ちの良い数式となっています。
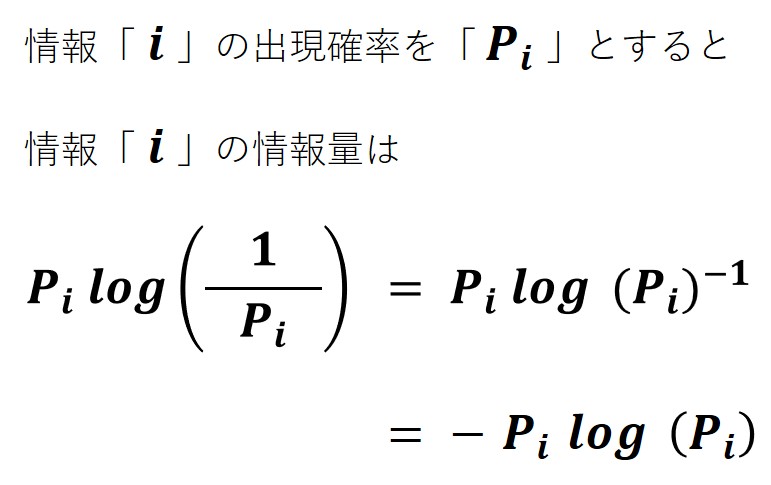
たとえば対数の底を 2 とすると、
カード「A(出現確率 3/4)」の情報量は
(3/4)✕ log2(1/(3/4)) = 0.311・・・
カード「B(出現確率 1/4)」の情報量は
(1/4)✕ log2(1/(1/4)) = 0.5
と計算されます。
二重課税のおかげで貧富の差が小さく見えるようになりました。
ここで、カード「A」と「B」の情報量を足し合わせると 0.811・・・となります。
これは悪魔がカード「A」と「B」を使って発信している 単位時間当たりの総情報量 ということになります。
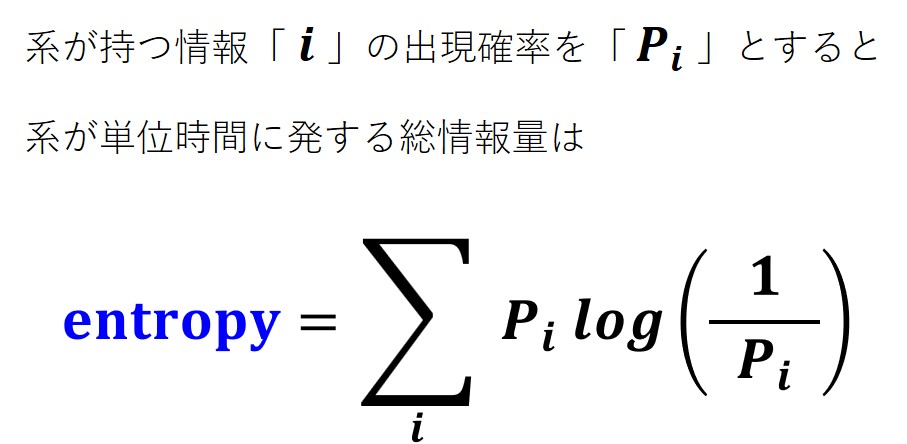
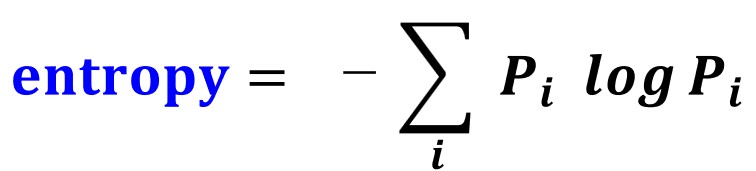
これを エントロピー と呼んでいます。
シグマの記号は覚えていますね。
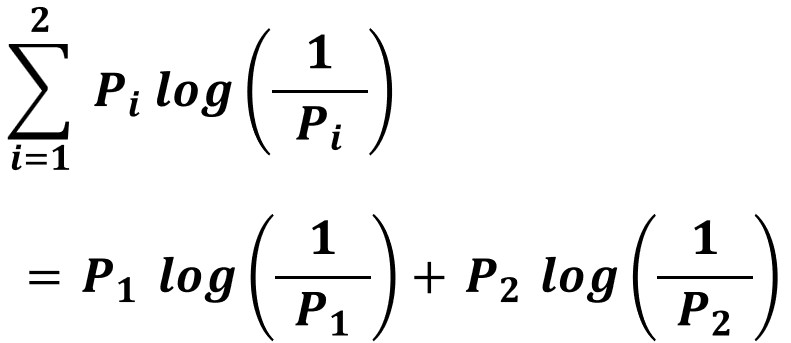
読まなくてよい注記:正統派の数学では「情報の希少価値」を「情報量」と呼び、その統計学的な「期待値」の計算式としてエントロピーを定義しています。補足(期待値):▶ ▶ ▶
しかし、ここでは、数学的なエントロピーも熱力学のエントロピーも同じものであるという立場からエントロピーの説明を試みています。試みなので失敗するかもしれません。
さて、カードでは実感がわきにくいでしょうから、スイカで説明します。
スイカが全部で4切れあります。
「A」の皿には普通に甘いスイカが3切れ、「B」の皿にはものすごく甘くて美味しいスイカが1切れあります。
均等な確率のくじ{A, A, A, B}を引いて、AもしくはBのスイカの皿をもらえるとき、「A(3切れ)」の価値を当たる確率( 3/4 )の逆数(すなわち 4/3 )あるいはその対数( log(4/3) )で考えることは妥当なことでしょう。
「B(すごく甘い1切れ)」の価値は当たる確率( 1/4 )の逆数( 4/1 )あるいはその対数( log(4/1) )で考えます。
味のことは無視して、「希少価値」だけで考えます。ここでは希少なスイカほど美味しく設定しただけのことです。希少なスイカほどマズく設定しても確率計算は同じであり、高価値となります。
しかし「A」にはスイカが3切れありますから、ノドが渇いているときは味以上に魅力的です。
そこで、先ほど計算した「A」の価値に、Aが当たる確率の大きさをかけて「A」の皿(スイカ3切れ)の魅力量とし、「B」価値に、Bが当たる確率の大きさをかけて「B」の皿(すごく甘いスイカ1切れ)の魅力量として、どちらがよいかを比較検討することは妥当なことだと考えられます。
「手に入る確率」✕「希少価値」=「魅力量」です。
もし「A」も「B」も頂ける場合は、各々の魅力量を足して総魅力量(=エントロピー)とします。
ではここで、いろいろな悪魔についてエントロピー(総情報量)を計算してみますが、先に、個々の確率、希少価値(確率の逆数をここでは底を 2 として対数化)、情報量(確率✕希少価値)について、確率の大小と情報量の大小関係を見ておきます。
| 対数の底=2 | ||
| 確率 | 希少価値 | 情報量 |
| 0.01 | 6.644 | 0.066 |
| 0.1 | 3.322 | 0.332 |
| 0.2 | 2.322 | 0.464 |
| 0.3 | 1.737 | 0.521 |
| 0.4 | 1.322 | 0.529 |
| 0.5 | 1.000 | 0.500 |
| 0.6 | 0.737 | 0.442 |
| 0.7 | 0.515 | 0.360 |
| 0.8 | 0.322 | 0.258 |
| 0.9 | 0.152 | 0.137 |
| 0.99 | 0.014 | 0.014 |
グラフで視覚的に大小関係を見てみます。
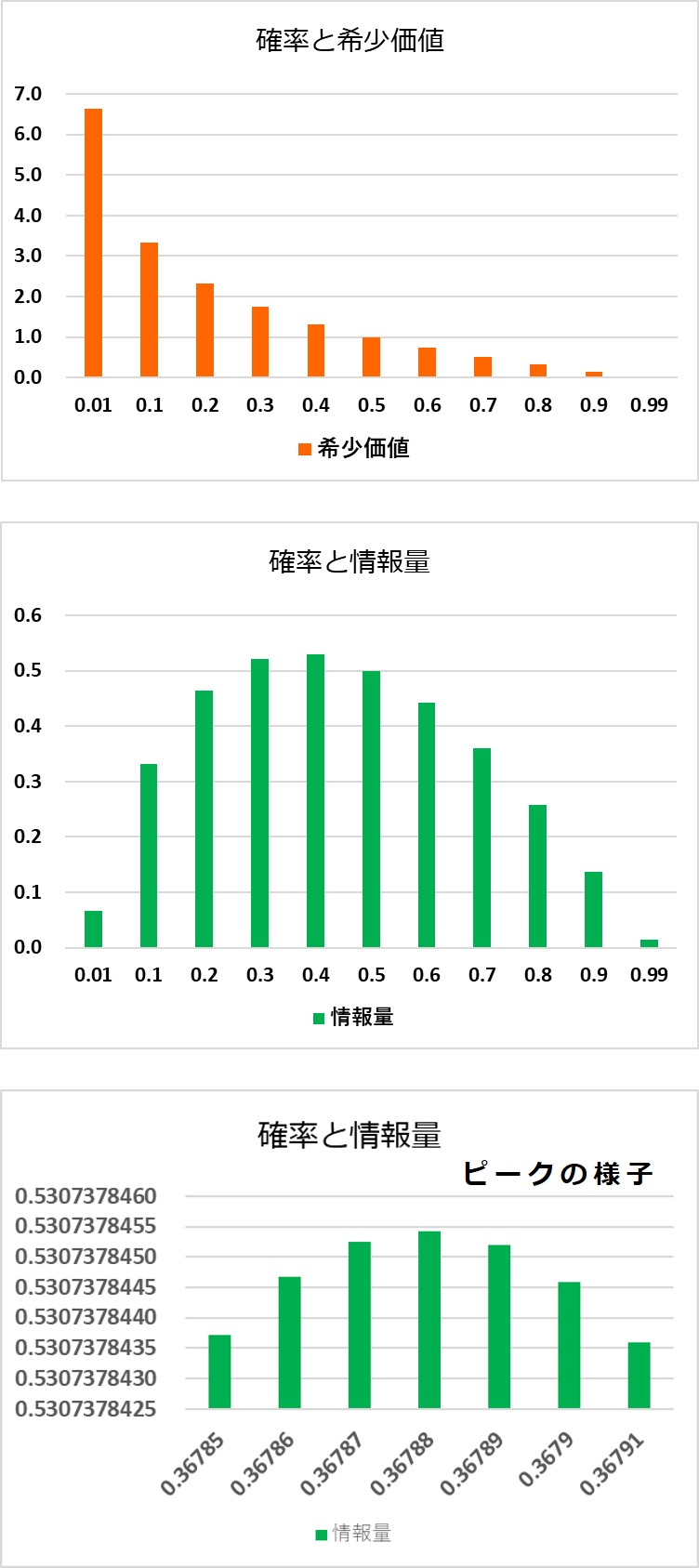
参考「メモ1」:▶ ▶ ▶
それでは、「A」と「B」という2種類の排他的な確率的現象の出現する系について、確率を変えながらエントロピー(総情報量)を計算してみます。
排他的:2つの事象が同時に発生しない状況
| 対数の底=2 | ||||
| 事象 | 確率 | 希少価値 | 情報量 | |
| A | 9/10 | 0.900 | 0.152 | 0.137 |
| B | 1/10 | 0.100 | 3.322 | 0.332 |
| 全体 | 1 | エントロピー | 0.469 | |
| 対数の底=2 | ||||
| 事象 | 確率 | 希少価値 | 情報量 | |
| A | 8/10 | 0.800 | 0.322 | 0.258 |
| B | 2/10 | 0.200 | 2.322 | 0.464 |
| 全体 | 1 | エントロピー | 0.722 | |
| 対数の底=2 | ||||
| 事象 | 確率 | 希少価値 | 情報量 | |
| A | 6/10 | 0.600 | 0.737 | 0.442 |
| B | 4/10 | 0.400 | 1.322 | 0.529 |
| 全体 | 1 | エントロピー | 0.971 | |
| 対数の底=2 | ||||
| 事象 | 確率 | 希少価値 | 情報量 | |
| A | 5/10 | 0.500 | 1.000 | 0.500 |
| B | 5/10 | 0.500 | 1.000 | 0.500 |
| 全体 | 1 | エントロピー | 1.000 | |
「等確率」のときに エントロピーが最大 になっているようです。
いろいろな確率で計算してグラフで確認してみます。
| A(確率:PA)、B(確率:1 - PA) | ||
| P | 1 - P | 系のエントロピー |
| 0.01 | 0.99 | 0.080793136 |
| 0.1 | 0.9 | 0.468995594 |
| 0.2 | 0.8 | 0.721928095 |
| 0.3 | 0.7 | 0.881290899 |
| 0.4 | 0.6 | 0.970950594 |
| 0.5 | 0.5 | 1 |
| 0.6 | 0.4 | 0.970950594 |
| 0.7 | 0.3 | 0.881290899 |
| 0.8 | 0.2 | 0.721928095 |
| 0.9 | 0.1 | 0.468995594 |
| 0.99 | 0.01 | 0.080793136 |
グラフにすると、等確率のときにエントロピーは最大 になっています。
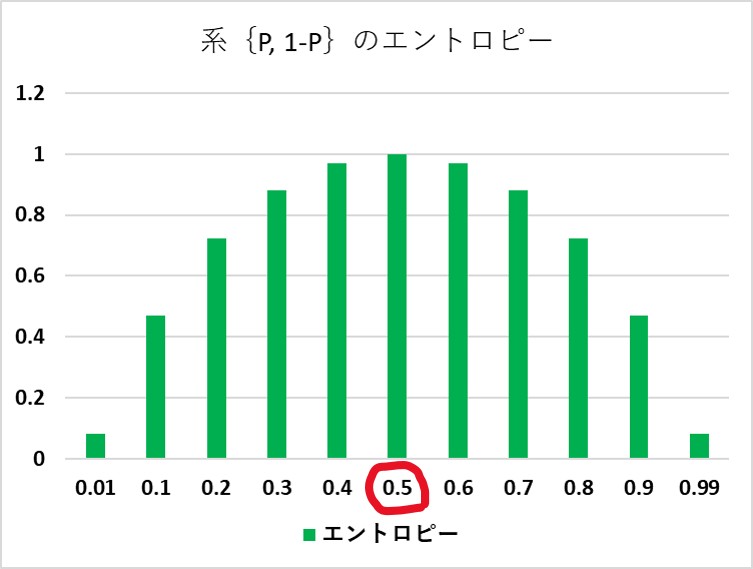
排他的な確率的現象の種類を増やしてみます。
| 対数の底=2 | ||||
| 事象 | 確率 | 希少価値 | 情報量 | |
| A | 6/9 | 0.667 | 0.585 | 0.390 |
| B | 2/9 | 0.222 | 2.170 | 0.482 |
| C | 1/9 | 0.111 | 3.170 | 0.352 |
| 全体 | 1 | エントロピー:→ | 1.224 | |
| 対数の底=2 | ||||
| 事象 | 確率 | 希少価値 | 情報量 | |
| A | 4/9 | 0.444 | 1.170 | 0.520 |
| B | 4/9 | 0.444 | 1.170 | 0.520 |
| C | 1/9 | 0.111 | 3.170 | 0.352 |
| 全体 | 1 | エントロピー | 1.392 | |
| 対数の底=2 | ||||
| 事象 | 確率 | 希少価値 | 情報量 | |
| A | 3/9 | 0.333 | 1.585 | 0.528 |
| B | 3/9 | 0.333 | 1.585 | 0.528 |
| C | 3/9 | 0.333 | 1.585 | 0.528 |
| 全体 | 1 | エントロピー | 1.585 | |
やはり確率が「等確率」のときに エントロピーは最大 になっているように見えます。
排他的な確率的現象の種類をさらに増やしてみます。
| 対数の底=2 | ||||
| 事象 | 確率 | 希少価値 | 情報量 | |
| A | 6/12 | 0.500 | 1.000 | 0.500 |
| B | 3/12 | 0.250 | 2.000 | 0.500 |
| C | 2/12 | 0.167 | 2.585 | 0.431 |
| D | 1/12 | 0.083 | 3.585 | 0.299 |
| 全体 | 1 | エントロピー | 1.730 | |
| 対数の底=2 | ||||
| 事象 | 確率 | 希少価値 | 情報量 | |
| A | 3/12 | 0.250 | 2.000 | 0.500 |
| B | 3/12 | 0.250 | 2.000 | 0.500 |
| C | 3/12 | 0.250 | 2.000 | 0.500 |
| D | 3/12 | 0.250 | 2.000 | 0.500 |
| 全体 | 1 | エントロピー | 2.000 | |
| 対数の底=2 | ||||
| 事象 | 確率 | 希少価値 | 情報量 | |
| A | 107/120 | 0.892 | 0.165 | 0.148 |
| B | 10/120 | 0.083 | 3.585 | 0.299 |
| C | 2/120 | 0.017 | 5.907 | 0.098 |
| D | 1/120 | 0.008 | 6.907 | 0.058 |
| 全体 | 1 | エントロピー | 0.602 | |
| 対数の底=2 | ||||
| 事象 | 確率 | 希少価値 | 情報量 | |
| A | 21/42 | 0.500 | 1.000 | 0.500 |
| B | 6/42 | 0.143 | 2.807 | 0.401 |
| C | 5/42 | 0.119 | 3.070 | 0.366 |
| D | 4/42 | 0.095 | 3.392 | 0.323 |
| E | 3/42 | 0.071 | 3.807 | 0.272 |
| F | 2/42 | 0.048 | 4.392 | 0.209 |
| G | 1/42 | 0.024 | 5.392 | 0.128 |
| 全体 | 1 | エントロピー | 2.199 | |
| 対数の底=2 | ||||
| 事象 | 確率 | 希少価値 | 情報量 | |
| A | 6/42 | 0.143 | 2.807 | 0.401 |
| B | 6/42 | 0.143 | 2.807 | 0.401 |
| C | 6/42 | 0.143 | 2.807 | 0.401 |
| D | 6/42 | 0.143 | 2.807 | 0.401 |
| E | 6/42 | 0.143 | 2.807 | 0.401 |
| F | 6/42 | 0.143 | 2.807 | 0.401 |
| G | 6/42 | 0.143 | 2.807 | 0.401 |
| 全体 | 1 | エントロピー | 2.807 | |
| 対数の底=2 | ||||
| 事象 | 確率 | 希少価値 | 情報量 | |
| A | 7/42 | 0.167 | 2.585 | 0.431 |
| B | 7/42 | 0.167 | 2.585 | 0.431 |
| C | 6/42 | 0.143 | 2.807 | 0.401 |
| D | 6/42 | 0.143 | 2.807 | 0.401 |
| E | 6/42 | 0.143 | 2.807 | 0.401 |
| F | 6/42 | 0.143 | 2.807 | 0.401 |
| G | 4/42 | 0.095 | 3.392 | 0.323 |
| 全体 | 1 | エントロピー | 2.789 | |
どうやら排他的な確率的現象の場合、等確率のときにエントロピーが最大値となる のは確かなようです。
数学的証明は割愛します(参照:【情報理論】情報源の情報量とエントロピーの計算問題:▶ ▶ ▶ 電気情報の森 2024.11.22)
おそらく無関係であり余計な着想ですが、貧富の差が無くなり完全に平均化すると国家の富は最大限になるが、「熱的死」に相当する状態を迎えるということかもしれません。
一方、常に貧富の差を作り出し、平均化に向かう動きを利用して構造を維持しているのが散逸構造として長く存続しえる国家です。
社会的不公平をすべて解消した社会は消え去るというパラドックスがあるのかもしれません。
では、次図のように「悪魔シャノン」と「悪魔ノイマン」が、お互いに調整することなく各々の手持ちから1枚のカードをそれぞれの確率でランダムに選び、同時に提示するということを繰り返すとき、「悪魔シャノン」のエントロピー、「悪魔ノイマン」のエントロピー、「悪魔シャノン&ノイマン」のエントロピーの関係を見てみます。
「A, B」は排他的(どれかひとつしか起こらない)、「C, D, E」は排他的です。
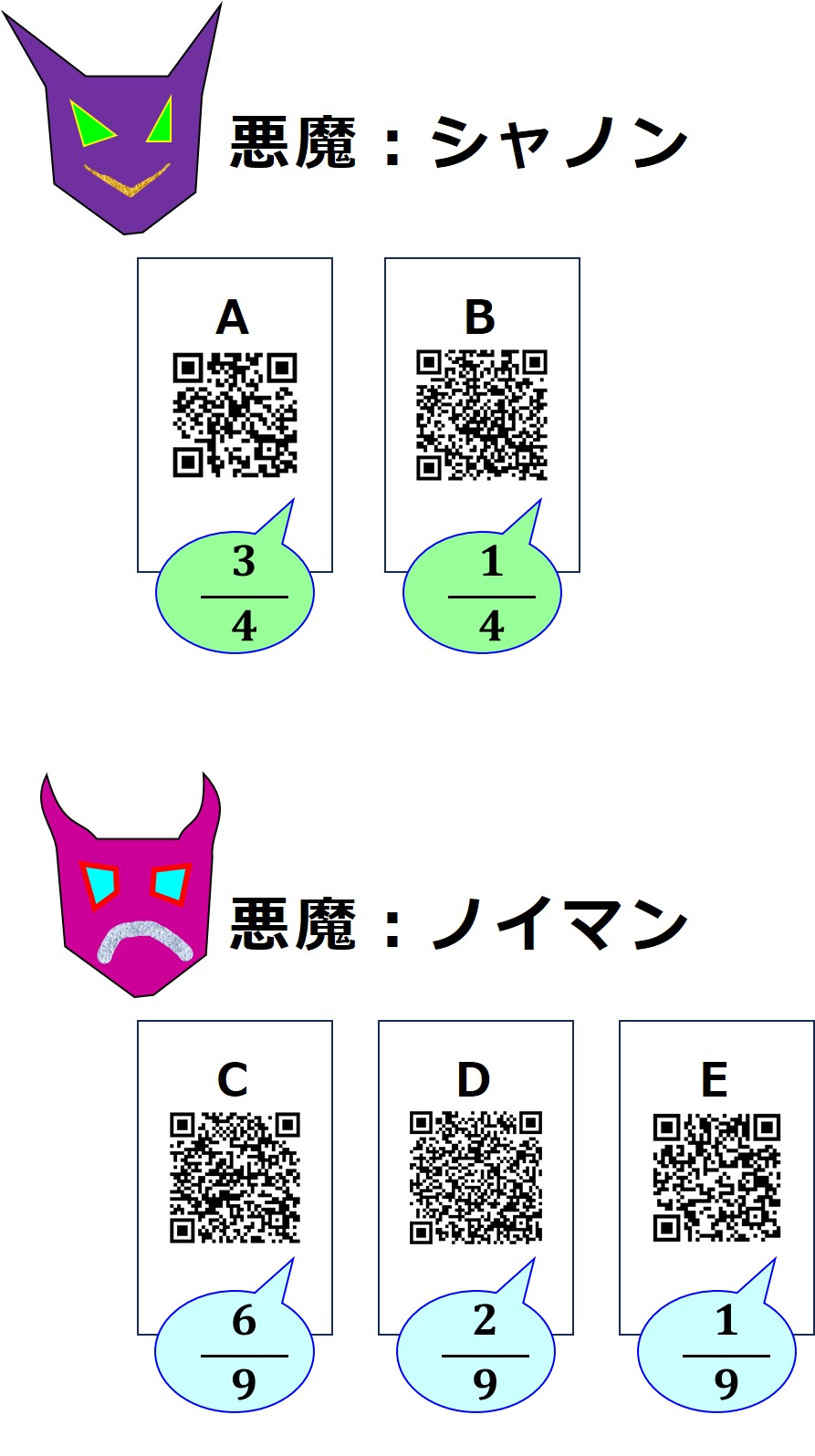
それぞれの計算表を示します。
| 悪魔シャノンのエントロピー(対数の底=2) | ||||
| 事象 | 確率 | 希少価値 | 情報量 | |
| A | 3/4 | 0.750 | 0.415 | 0.311 |
| B | 1/4 | 0.250 | 2.000 | 0.500 |
| 全体 | 1 | エントロピー | 0.811 | |
| 悪魔ノイマンのエントロピー(対数の底=2) | ||||
| 事象 | 確率 | 希少価値 | 情報量 | |
| C | 6/9 | 0.667 | 0.585 | 0.390 |
| D | 2/9 | 0.222 | 2.170 | 0.482 |
| E | 1/9 | 0.111 | 3.170 | 0.352 |
| 全体 | 1 | エントロピー | 1.224 | |
単純に「悪魔シャノンのエントロピー 0.811」と「悪魔ノイマンのエントロピー 1.224」を合計すると 2.035 になります。
「悪魔シャノン&ノイマン」のエントロピーは、ここでは「AとC」、「AとD」のように2匹の悪魔の示すカードの組み合わせで計算します。また「AとC」が提示される確率は「Aが出てくる確率」✕「Cが出てくる確率」で計算します。
| 悪魔シャノン&ノイマンのエントロピー(底=2) | ||||
| 事象 | 確率 | 希少価値 | 情報量 | |
| AC | 18/36 | 0.500 | 1.000 | 0.500 |
| AD | 6/36 | 0.167 | 2.585 | 0.431 |
| AE | 3/36 | 0.083 | 3.585 | 0.299 |
| BC | 6/36 | 0.167 | 2.585 | 0.431 |
| BD | 2/36 | 0.056 | 4.170 | 0.232 |
| BE | 1/36 | 0.028 | 5.170 | 0.144 |
| 全体 | 1 | エントロピー | 2.036 | |
ここに「悪魔ボルツマン」がやってきて、2匹の悪魔からカードを奪い取りました。
「悪魔シャノン」と「悪魔ノイマン」の区別を無視して、5種類のカードの出現確率だけを見てエントロピーを計算しても同じことになります。
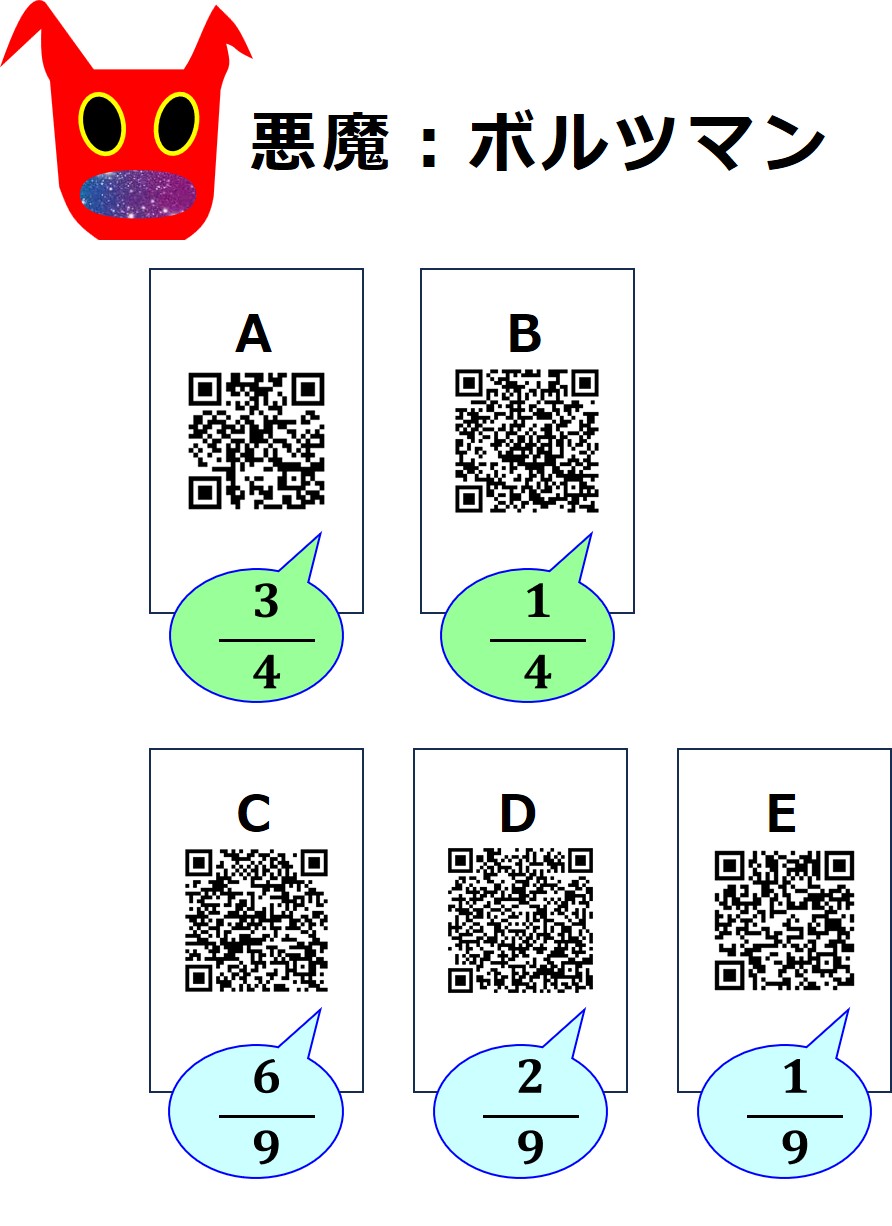
| 悪魔ボルツマンのエントロピー(対数の底=2) | ||||
| 事象 | 確率 | 希少価値 | 情報量 | |
| A | 3/4 | 0.750 | 0.415 | 0.311 |
| B | 1/4 | 0.250 | 2.000 | 0.500 |
| C | 6/9 | 0.667 | 0.585 | 0.390 |
| D | 2/9 | 0.222 | 2.170 | 0.482 |
| E | 1/9 | 0.111 | 3.170 | 0.352 |
| 全体 | 1 | エントロピー | 2.036 | |
「悪魔シャノン」のエントロピー 0.811 と「悪魔ノイマン」のエントロピー 1.224 との合計 2.035 が「悪魔シャノン&ノイマン」や「悪魔ボルツマン」のエントロピー 2.036 になっています。(小数点第3位のズレは四捨五入によるものです)
確率的に出現する事象を持つ系が複数個あり、それぞれの系の確率的出現が互いに独立しているとき、複数個の系全体のエントロピーはそれぞれの系のエントロピーの単純な合計になります。
計算が簡単でよいですね。
なお、事象が1種類のときは、「情報量 = エントロピー」となります。正統派の定義に従わない場合。
| 対数の底=2 | ||||
| 事象 | 確率 | 希少価値 | 情報量 | |
| A | 1/4 | 0.250 | 2.000 | 0.500 |
| 全体 | 1 | エントロピー | 0.500 | |
では大事なことをまとめておきます:

ちょっとした気づきをメモとして残しておきます。将来の研究に使えるかもしれないヒントのようなものです。
次の図を見て気になったこと:0.36788 ってヒトの体温?(平熱)

水が液体のとき、水分子が仮に「情報発信B」というものを持っているとします。
この「情報発信B」は水温 0℃で「確率=0」、水温 100℃で「確率=1」を持つとします。
すると「情報発信B」は水温 36.8℃あたりで最大情報量を持つことになります。
これはヒトの体温と関係あるでしょうか? それとも無関係でしょうか?
そのような「情報発信B」は、いったい何なのでしょうか?
ちなみに、ヒトの平熱は37℃あたりですが、激しい活動をしているときは40℃を越えます。
水の比熱が最小になるのは43℃あたりのようです。
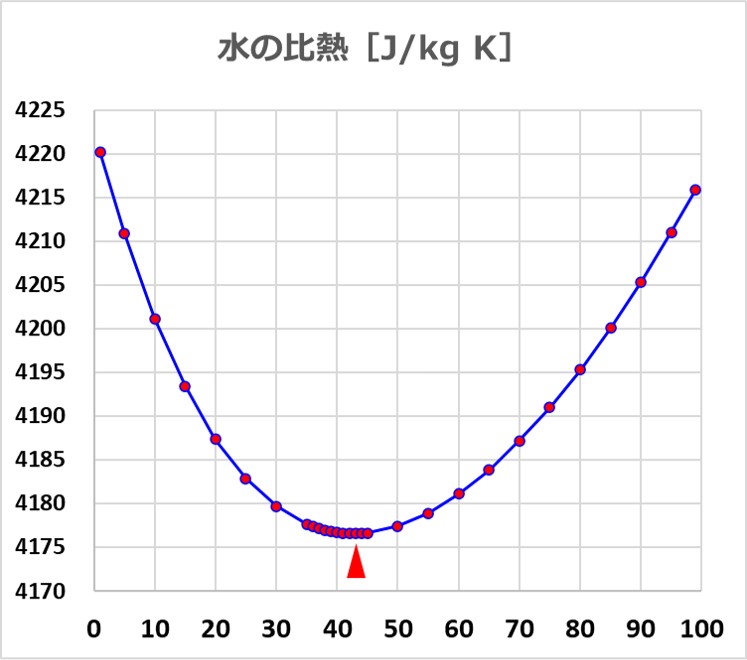
参考:Sience.Tools 科学技術計算ツール(CATTech.LAB Co. 2019.09.11)
多くの学者が体温の説明を試みていますが、最終的には(効率の問題として)エントロピーで説明されるのかもしれませんね。😄
箱の中にクジ引きの券が2枚入っているとします。1枚は100円、もう1枚は200円当たるとすると、箱からクジ引きを1枚取るときの「期待値」は 100 ✕(1/2) + 200 ✕(1/2) = 150 円と計算します。
実際に当たってもらえるのは 100 円か 200 円のどちらかです。
箱の中にクジ引きの券が4枚入っているとします。3枚は100円、もう1枚は200円当たるとすると、箱からクジ引きを1枚取るときの「期待値」は 100 ✕(3/4) + 200 ✕(1/4) = 125 円と計算します。
実際に当たってもらえる 100 円か 200 円かは「意味」です。これを「情報(の確率的な希少価値)」に置き換えます。
100 円は確率 3/4 なので逆数化して 4/3 または更に対数化して log(4/3) 、200 円は確率 1/4 なので 逆数化して 4/1 または更に対数化して log(4/1)
通常は対数を用いるので、例えば対数の底を 2 として期待値の計算式を用いると エントロピー を log(4/3) ✕(3/4) + log(4/1) ✕(1/4) = 0.811・・・ と計算します。
エントロピーの計算式を見てわかるように、100円とか200円とかの「意味」は使っていません。使っているのは「確率」のみです。
なお、エントロピー計算では確率を前に置いて (3/4)log(4/3) + (1/4)log(4/1) = 0.811・・・ と記述します。
また、正統派数学では log(4/3) を情報量と呼んでいますが、このページでは (3/4)log(4/3) を情報量としています。
エントロピーの迷宮に嵌り込みたい方向けの参考:「第2問題」:▶ ▶ ▶
身の回りのあらゆる情報は、構造と言い換えることができ、分布の偏りと言い換えることもできますが、(もう宇宙の始まりのときではないので)宇宙全体の中で静止することなく変化し続けています。
ある構造が宇宙全体に均等に拡がり、分布の偏りが無くなって静止すれば、宇宙全体の背景に埋没して消えることになるので関心を向ける価値はないでしょう。
したがって、身の回りのあらゆる情報(=構造、=分布の偏り)はエントロピーを持っています。
目で見て得た情報、耳で聴いて得た情報、触って得た情報などが、ヒトの脳の中で再構築され意味づけされて、自分の周りの世界の構造が認識されています。
英語では、生の情報をデータ、意味づけされた情報をインフォメーションと呼んで区別するそうです。
ここで扱うのは生の情報(データ)です。
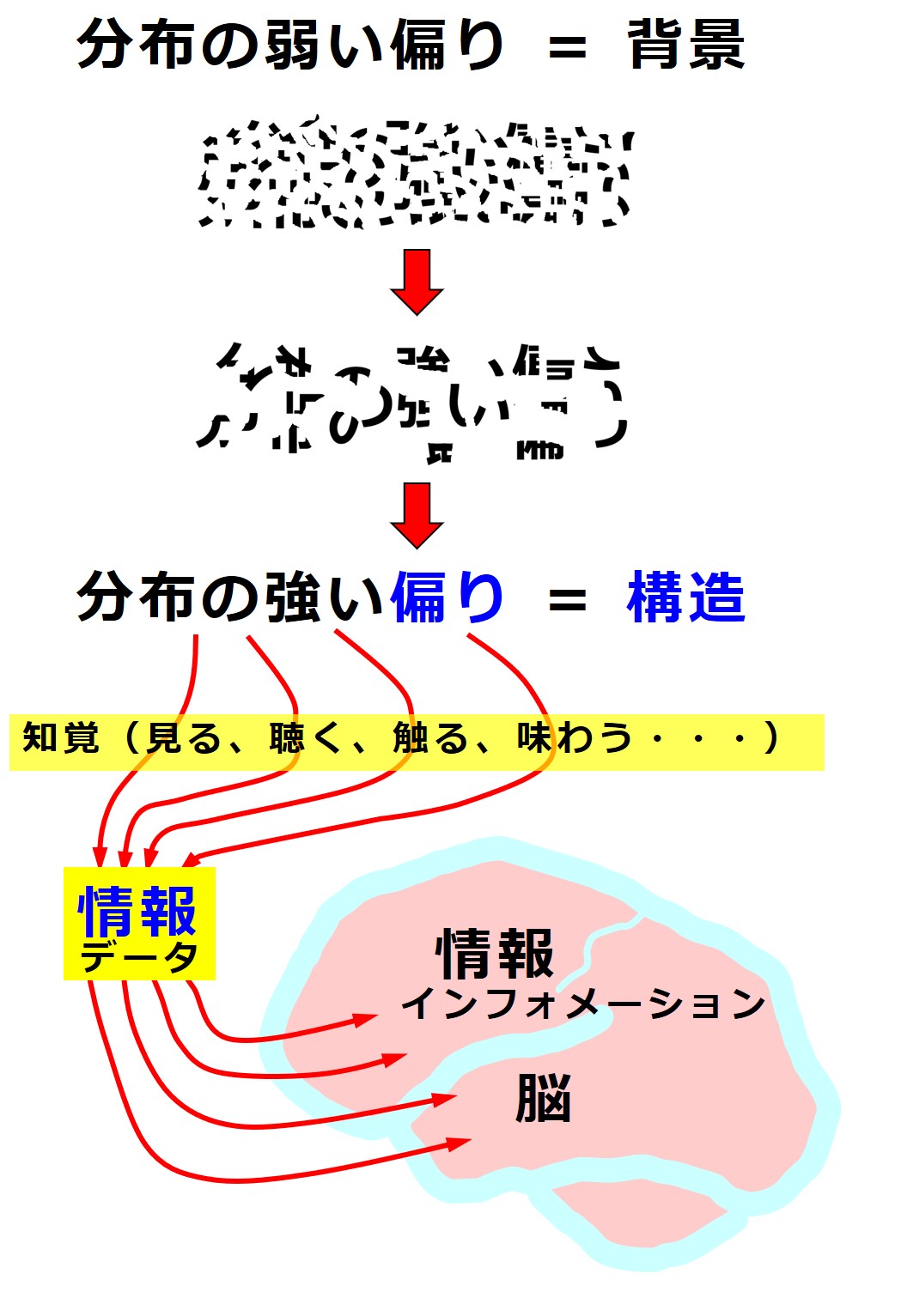
私たちが知っているあらゆる物は何らかの構造を持っています。
構造は何らかの分布の偏り(=情報)ですから、あらゆる物は情報であり、エントロピーを持っています。
1kgの金塊は、キラキラしてずっしりと重く、とても魅力的ですが、この金塊は物体であり、同時に情報の塊なのです。
金塊を物体と捉えているのはヒトの脳の働きによる感覚的なものであり、「一種の錯覚のようなもの」です。
金塊のまぎれもない実体は、情報のかたまりであり、金塊はエントロピーを持っています。
金塊がどんな情報(=構造)を持っているか、究極的なことはまだわかっていないようです。
金塊を分解するなどの実験的研究で、金の原子が見つかり、原子の分解で原子核や電子が見つかり、さらに分解を続けていろいろな素粒子などが見つかっていくといったことが繰り返されてきましたが、・・・どこまで行くのかはわかりませんが・・・どのような構造も情報であり、エントロピーを持っています。
「物質は実体があり、情報は幽霊」というような世界観を持っているならば、捨てましょう。
「実体の感覚(実在感)」は脳が作り出している錯覚です。
もし情報が実体を伴わない幽霊だと言うのであれば、全世界が幽霊です。
さて、この情報を担う「実体的なもの」を エネルギー と呼んでいます。
ヒトの脳が「実在している」と意味づけを与えているあらゆるものがエネルギーであり、具体的には、物質と呼ばれているもの、波と呼ばれているものなど、ありとあらゆるものが情報を担っているエネルギーです。
それらはすべて「〇〇エネルギー」と呼ばれています:運動エネルギー、位置エネルギー、電気エネルギー、結合エネルギー、太陽エネルギー、熱エネルギーなど。
「〇〇エネルギー」と呼ばれているあらゆるものが、いわば 情報の運搬体(キャリアー) であり、エントロピーを持っています。
そしてエントロピーを持つあらゆるものは「○○エネルギー」と呼べるものです。
私たちの住む世界は、エネルギーだらけ、エントロピーだらけです。
さて、クラウジウス という人は熱力学の実験をしていて 熱エネルギーのエントロピー を発見しました(1865年頃)。
これは科学が発見した最初のエントロピーです。
クロード・シャノン という人は通信の効率について数学的研究をしていて 情報理論のエントロピー を発見しました(1949年頃)。
このウェブページで最初に紹介しているエントロピーです。
エントロピー発見の歴史的な順番による影響を受けて、熱エネルギーのエントロピーと情報理論のエントロピーは、中身は別ものとして扱われてきました。
これから、(エレガントな方法ではありませんが、基本に沿って)クラウジウスのエントロピーの計算式を導き出します。
地球による重力が働いている所に冷水の満たされた水槽があるとします。底の方にある水を熱して温水に変えます。

温水では水分子同士の距離が拡がり密度が低くなっているので上に向かって移動します。温水に押し出された冷水は下に向かって移動します。
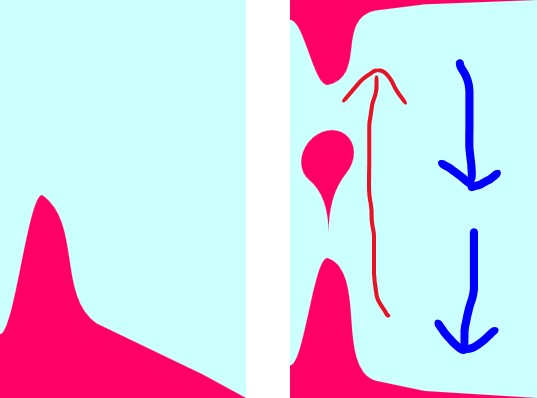
このとき途中に歯車を置くと水流で回転しますから、それでモーターを回すと発電します。
しかし、歯車を置かないで放置した場合、対流などで温水と冷水が混じり合い、長い時間をかけて最終的には均一な温度の水になります。
歯車を置いていた場合も均一な温度に近づいて対流がなくなれば、歯車は止まります。最終的な温度は歯車を置かない場合よりも低くなります。
20 ℃の水 1 Lと40 ℃の水 1 Lを混ぜると、細かいことは抜きにして、30 ℃の水 2 Lができます。
これを利用して水に加える熱エネルギーと増えるエントロピーとの関係を見てみます。
ここでは、情報のエントロピーの数式から無理やりクラウジウスの熱エントロピーの数式を導きたいと思います。
まず水(液体)の熱は、水分子の振動や回転、水分子から放出されている赤外線などさまざまなもので構成されています。
水(液体)は、熱に関して「情報発信A1」、「情報発信A2」、「情報発信A3」・・・と様々な構造が情報を発信し、エントロピーを持っていると考えられます。
ここで扱うのは、それらの情報発信のうち最も主たるものであり「情報発信A1」と呼んでおきます。
さて「情報発信A1」の出現確率は不明ですが、水温 1 ℃ ~ 99 ℃のときの出現確率として「0.01 ~ 0.99」を対応させると、次図のようにマズいことになります。
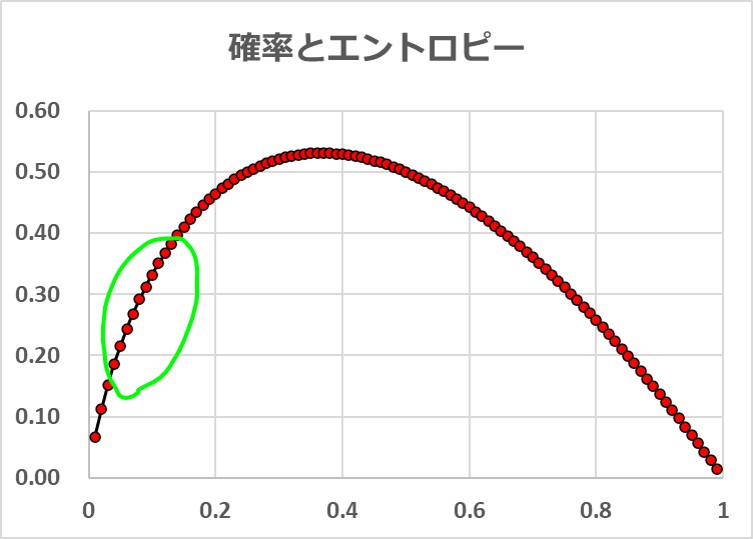
そこで、エントロピーがほぼ直線的に増加している部分の確率を「情報発信A1」の「水温 1 ℃ ~ 99 ℃」に対応する出現確率とします。
ここでは次表のように「水温 1 ℃ ~ 99 ℃」に出現確率「0.001 ~ 0.099」を当てました。
表の真ん中のTが水温(℃)です。左端の列は「1/T」の累計です。エントロピーはSで表記しています。「ΔS」は、温度が 1 ℃増えたときのエントロピーの増分です。
ここでは、温度による比熱の違いなどは無視して 1 カロリーの熱エネルギーで温度が 1 ℃上がるとしています。
したがって、Tは 温度を上げるために投与した熱エネルギー Q の累計となっています。
また、関係性を見たいだけなので単位とかは無視しています。
表の各項目を選んだ理由は:種明かしもクソもない話ですが、クラウジウスの数式に相当する項目を選んでいます。
| 1/T 累計 | 1/T | T ℃ | 確率 | S | ΔS |
| 1.000 | 1.000 | 1 | 0.001 | 0.010 | 0.008 |
| 1.500 | 0.500 | 2 | 0.002 | 0.018 | 0.007 |
| 1.833 | 0.333 | 3 | 0.003 | 0.025 | 0.007 |
| 2.083 | 0.250 | 4 | 0.004 | 0.032 | 0.006 |
| 2.283 | 0.200 | 5 | 0.005 | 0.038 | 0.006 |
| 2.450 | 0.167 | 6 | 0.006 | 0.044 | 0.006 |
| 2.593 | 0.143 | 7 | 0.007 | 0.050 | 0.006 |
| 2.718 | 0.125 | 8 | 0.008 | 0.056 | 0.005 |
| 2.829 | 0.111 | 9 | 0.009 | 0.061 | 0.005 |
| 2.929 | 0.100 | 10 | 0.010 | 0.066 | 0.005 |
| ~ | ~ | ~ | ~ | ~ | ~ |
| 5.136 | 0.011 | 95 | 0.095 | 0.323 | 0.002 |
| 5.147 | 0.010 | 96 | 0.096 | 0.325 | 0.002 |
| 5.157 | 0.010 | 97 | 0.097 | 0.326 | 0.002 |
| 5.167 | 0.010 | 98 | 0.098 | 0.328 | 0.002 |
| 5.177 | 0.010 | 99 | 0.099 | 0.330 | - |
グラフにすると次図のようになります(温度による比熱の違いを考慮しても似たようなグラフになるので省略します)。
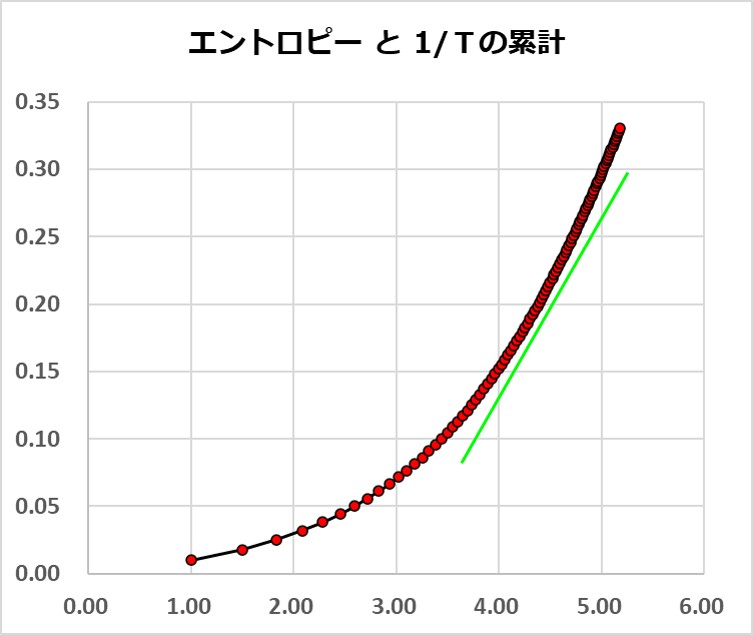
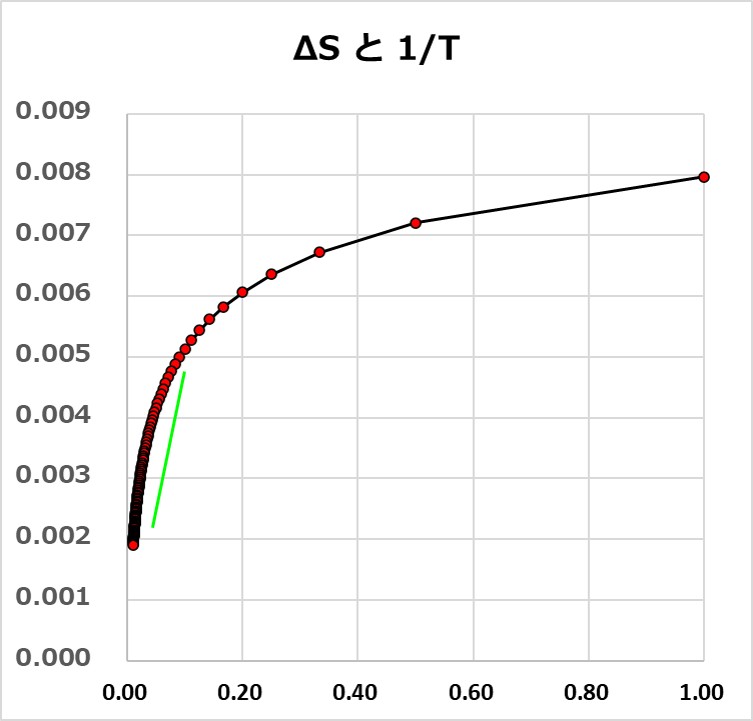
着目するのはドットが集中している直線部分です。
最後のグラフの直線部分はクラウジウスの熱エントロピーの式「 ΔS = ΔQ/T 」となっています。
ゴールが見えているので簡単でしたね。
終わりです 💀
無理やりやっつけた感じですが、大事なことは、熱力学のエントロピーも情報理論のエントロピーも本質的に同じもの(つまり何らかの情報発信)を扱っているということです。将来は賢い学者さんによってもっとエレガントな導出が行われるでしょう。
クラウジウスの後は、ルートヴィッヒ・ボルツマンによってエントロピーの解釈が現れました。また情報理論でも、シャノン以外にも色々なエントロピー計算式が提案されています。
では、異なる温度の水を混ぜて、温度やエントロピーの変化を見てみましょう。
10 ℃の水と 30 ℃の水を等量混ぜた直後のエントロピーを、混合が進み均一な温度(20 ℃)になったときのエントロピーの大きさと比較します。
| 10 ℃ 1 L | |||
| 事象 | 確率 | 希少価値 | 情報量 |
| A | 0.01 | 6.644 | 0.066 |
| B | 0.01 | 6.644 | 0.066 |
| C | 0.01 | 6.644 | 0.066 |
| 全体 | エントロピー | 0.199 | |
| 30 ℃ 1 L | |||
| 事象 | 確率 | 希少価値 | 情報量 |
| D | 0.03 | 5.059 | 0.152 |
| E | 0.03 | 5.059 | 0.152 |
| F | 0.03 | 5.059 | 0.152 |
| 全体 | エントロピー | 0.455 | |
| 10 ℃ 1 L + 30 ℃ 1 L | |||
| 全体 | エントロピーの合計 | 0.654 | |
| 20 ℃ 2 L | |||
| 事象 | 確率 | 希少価値 | 情報量 |
| A | 0.02 | 5.644 | 0.113 |
| B | 0.02 | 5.644 | 0.113 |
| C | 0.02 | 5.644 | 0.113 |
| D | 0.02 | 5.644 | 0.113 |
| E | 0.02 | 5.644 | 0.113 |
| F | 0.02 | 5.644 | 0.113 |
| 全体 | エントロピー | 0.677 | |
「10 ℃ 1 L + 30 ℃ 1 L」は、温度分布に偏りがあります。均等な「20 ℃ 2 L」になることによってエントロピーは大きくなっています。
「10 ℃ 1 L + 30 ℃ 1 L」がその分離状態を保つことは基本的にはありません。必ず混合が進んで「20 ℃ 2 L」になります。
「20 ℃ 2 L」を放置しても、勝手に「10 ℃ 1 L + 30 ℃ 1 L」と分離することはまず起こりえません。
この一方的な変化の根源にあるものを数学では「大数の法則(中心極限定理)」と呼び、物理学では「熱力学第2法則(エントロピー増大の法則)」と呼んでいますが、本質的には同じことです。
「確率的な現象では、確率の大きなものがたくさん起こりやすい」という小泉進次郎の名言のようなことを言っているだけのことです。
いろいろな説明を省略しているので難しいかもしれません。後日補足していきます。
散逸構造について説明します。
まず、エントロピーの移動について説明します。
次のような予想を立ててみます。

異なる物質の間でも移動しやすいエントロピーの代表は「熱エントロピー」です。
室温下で水の入った鍋を熱い鉄板の上に置くと(ガス台に置いて火をつけてもかまいません)、鉄板の熱エントロピーは鍋の水に移動し始めます。この熱エントロピーの移動は両者の温度が等しくなるまで続きます。
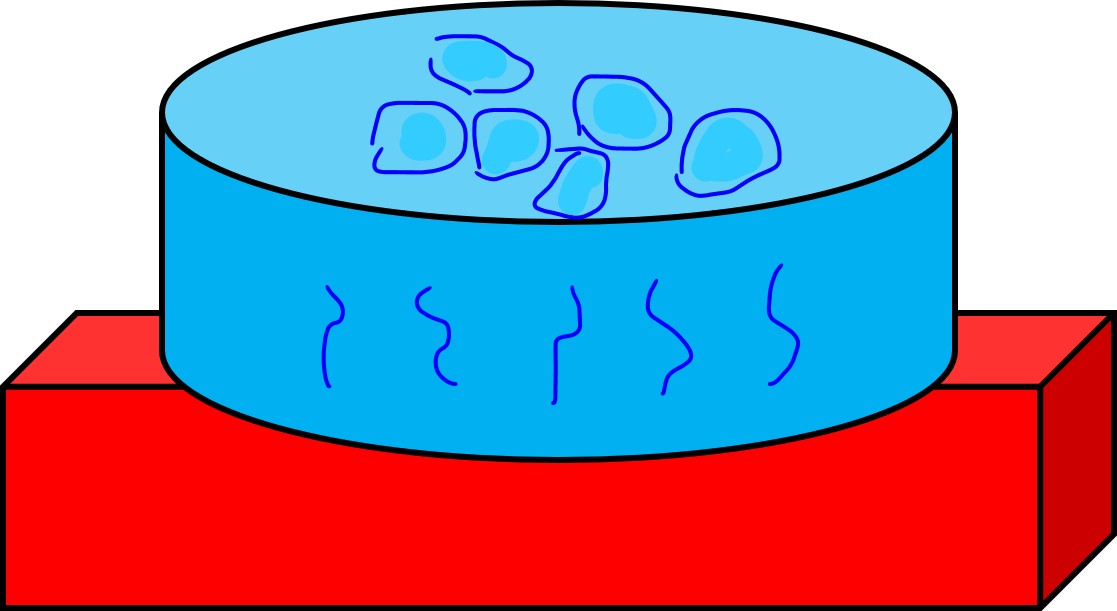
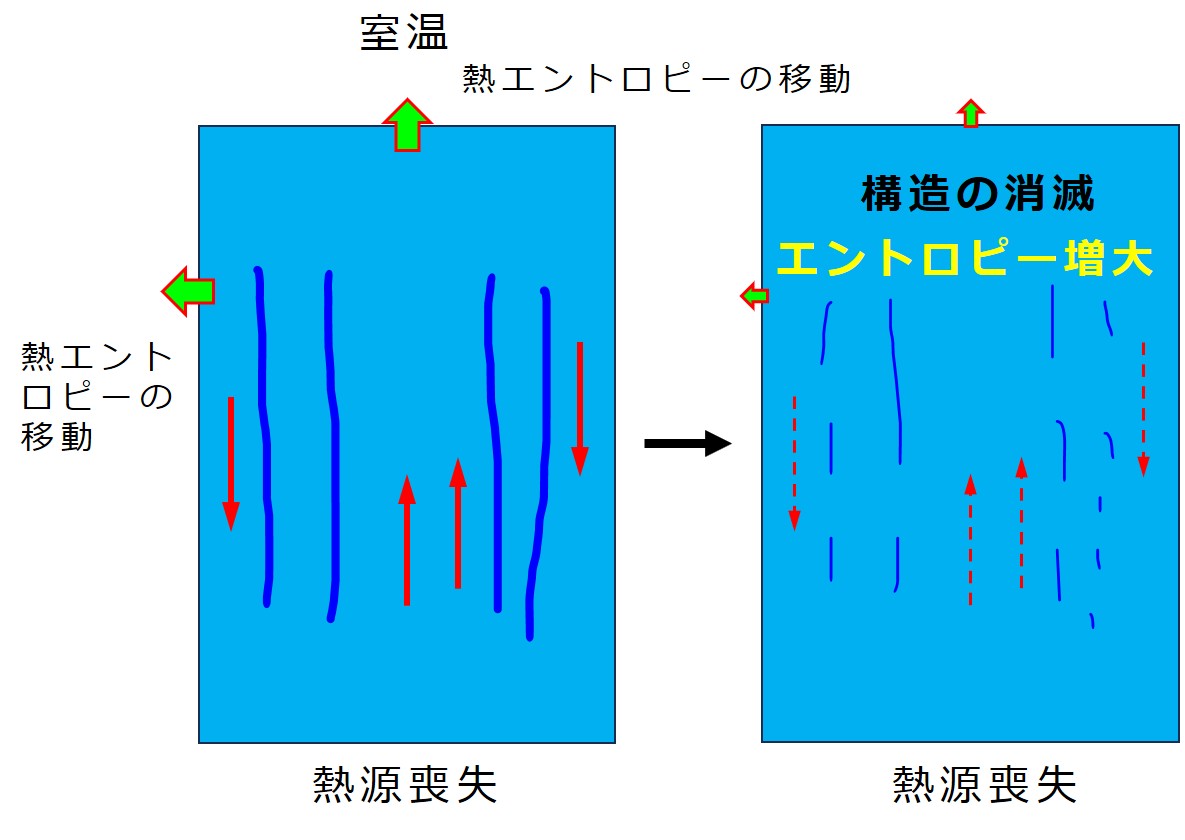
熱エントロピーが移動中、水の中に模様(ここでは対流構造)が現れます。
この模様は、熱エントロピーの移動が無くなると消えます。
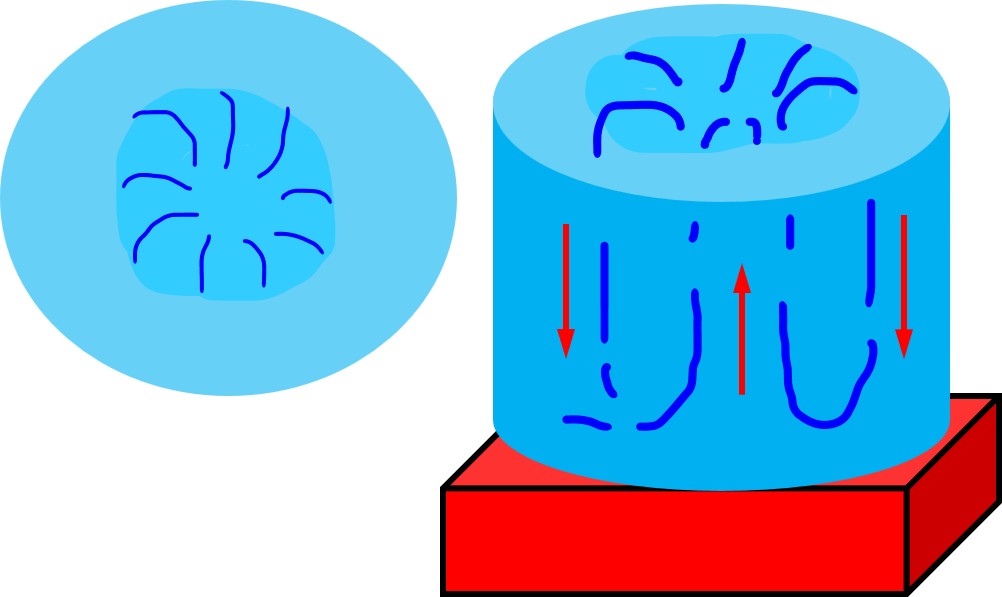
このような模様(構造)のことを 散逸構造(さんいつこうぞう)と呼びます。
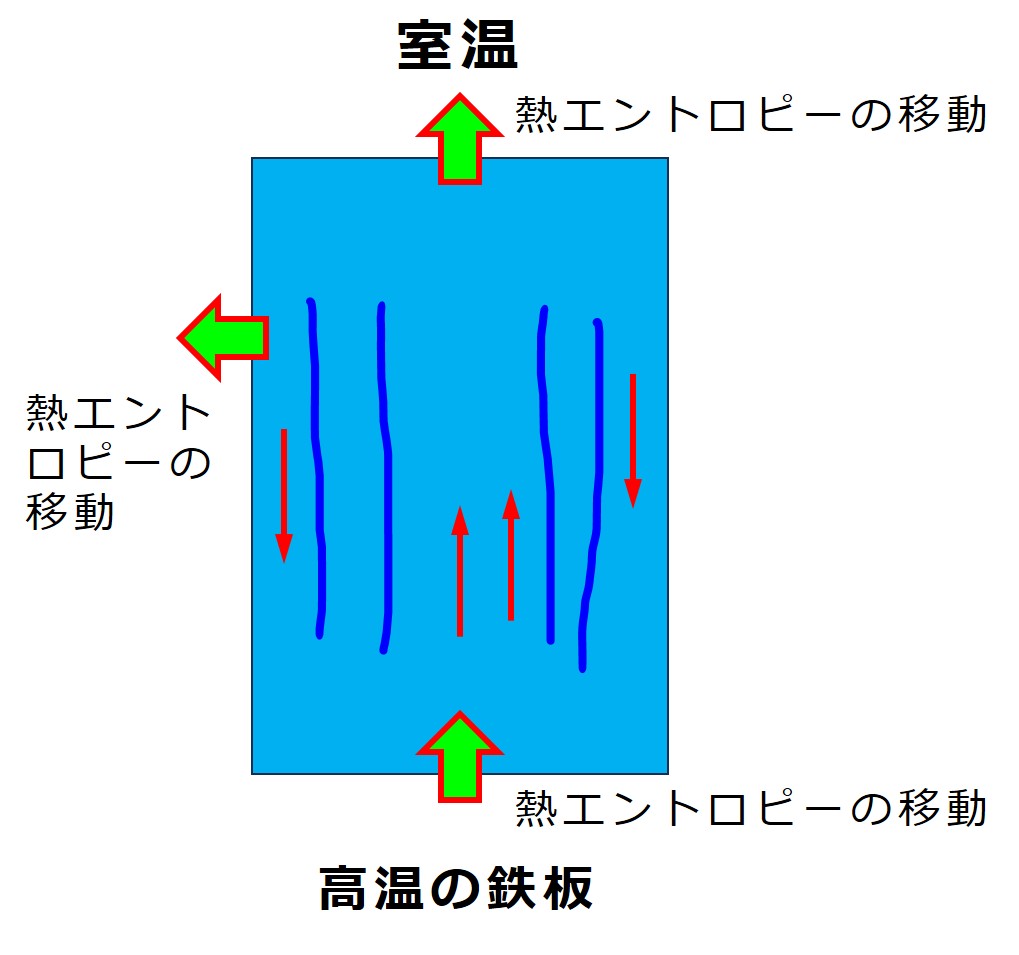
鉄板が取り除かれるなどによりエントロピーの移動が途絶えると散逸構造は消滅します。その散逸構造自身が持つエントロピーは崩壊時に増大します。
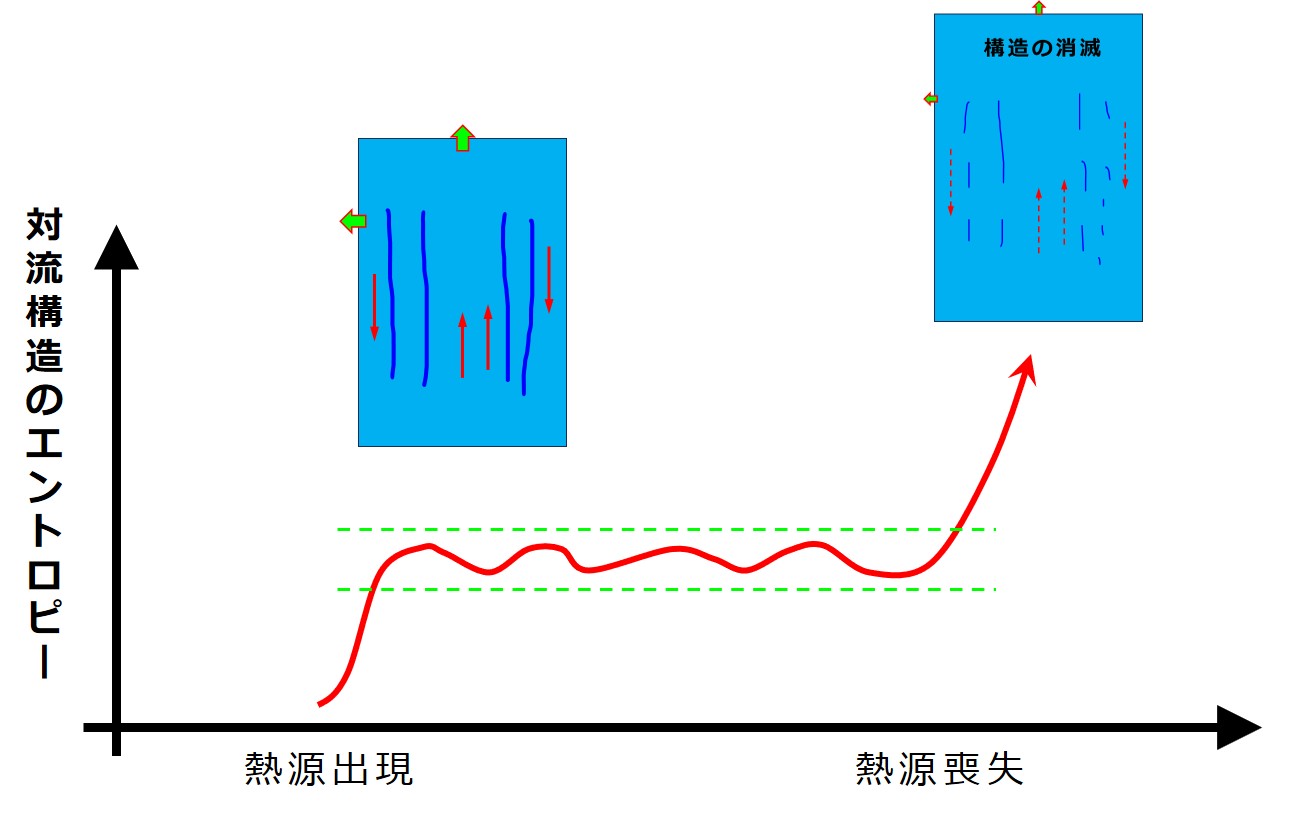
ここで「第3説明」の図をもう一度並べます。




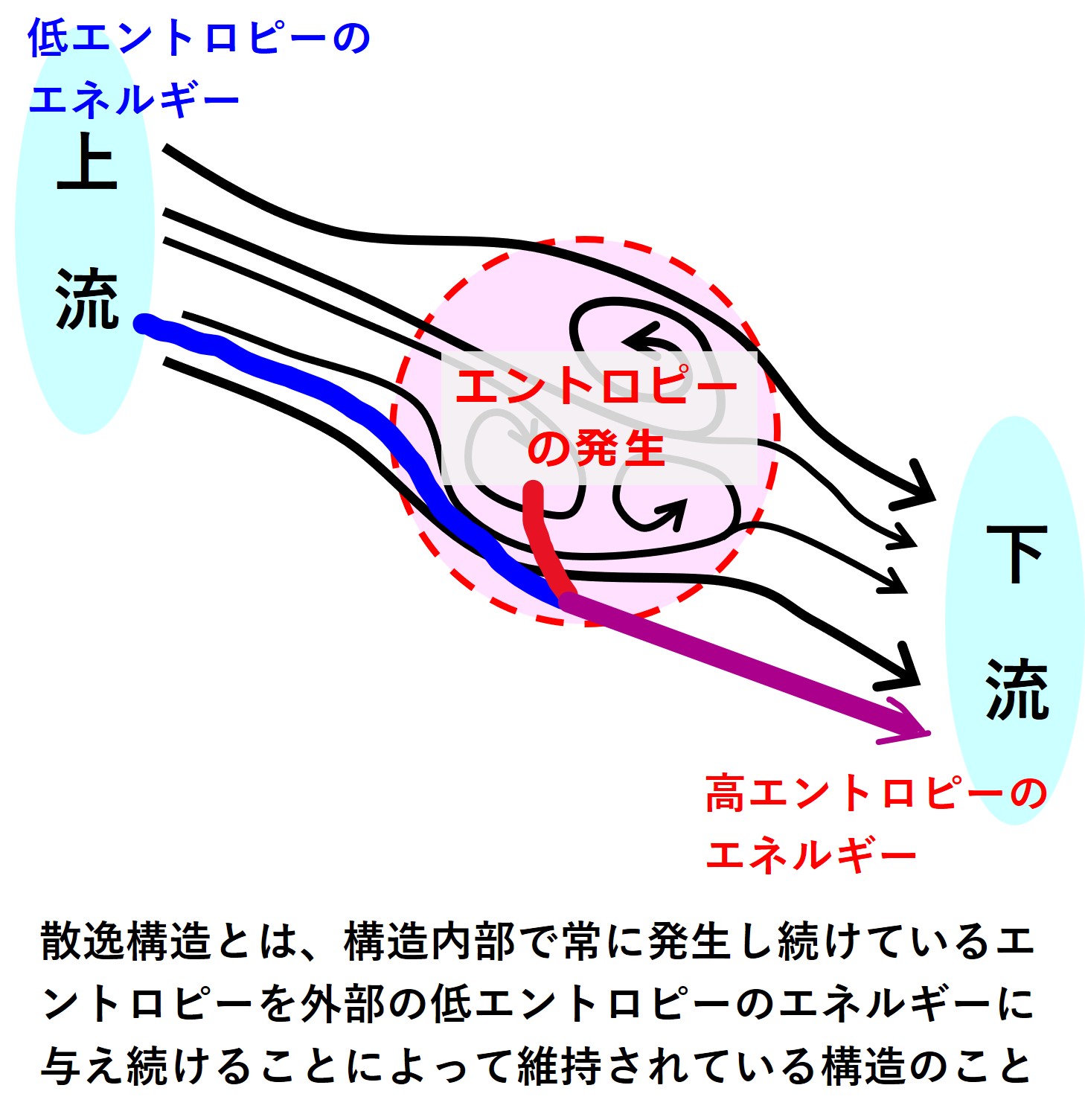
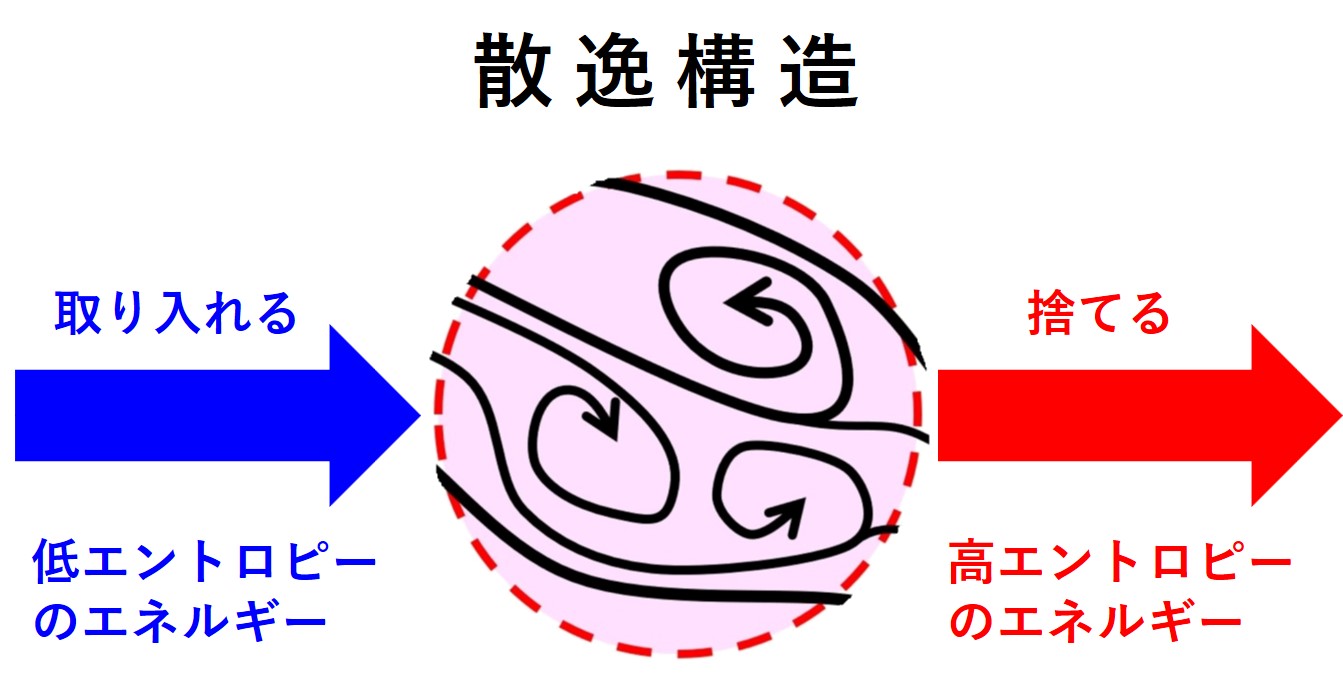
散逸構造の中では常にエントロピーが増大し、構造が壊れています。散逸構造は増大するエントロピーを他のエントロピー運搬体に渡すことにより処理して現在の構造を維持しています。
散逸構造の身近な例は、生き物です。環境から「低エントロピーのエネルギー(食料など)」を取り入れて「高エントロピーのエネルギー(ウンチや炭酸ガスなど)」を放出しています。
一般的に「寿命」のあるものはすべて散逸構造です。
国家もそうです。日本もやがて滅亡の日を迎えることでしょう。構造を守るという努力が無くなれば滅亡の日は早まることでしょう。
宗教や思想も散逸構造です。構造を守るための努力が無くなれば消滅します。
イリヤ・プリゴジンという学者が散逸構造論でノーベル賞を受賞したとき、キリスト教の某お偉方が「これは素晴らしい考え方だが、あらゆるものに適用できると考えるべきではない」とクギをさしたそうです。
散逸構造論は、あらゆるものに適用できます 😄
どういう条件で散逸構造が残り、あるいは消えていくのか、チャールズ・ダーウィンの進化論と組み合わせて考えれば「最強の世界観」を得ることができます。
まっ、日本人は大昔から知っていることです。
エントロピーとか難しすぎると感じる日本人は、あえて散逸構造論や進化論を勉強する必要はありません。
余談です。
私がなぜこのページを作ったのか、その背景説明です。
「自然界に多く見られるフィボナッチ数や黄金比などは、自然界の数量的な系の最大エントロピー(または最小エントロピー)を意味しているというテーマ」で研究をやっていました。
研究というよりは、素人の私がアイデアを出して専門家からコメントを得るということをやっていました(その当時に作ったページ:▶ ▶ ▶)。
コロナ騒動が始まってから、コロナが面白いので忙しくなり、しばらくフィボナッチやエントロピーとはご無沙汰だったのですが、令和7年2025年の夏、メールボックスを整理していて「Fibonacci & Maximum Entropy (Implicit Information) - Entropy Begets Design - Asynsis Principle(2024.03.31)」というメールに気づきました。
2020年ノーベル物理学賞を受賞したロジャー・ペンローズという人が量子脳理論というのを唱えています。
彼は意識の宿る場として神経細胞内にある微小管というものに着目しているらしいのですが、この微小管はチューブリン13個を単位としているようです。
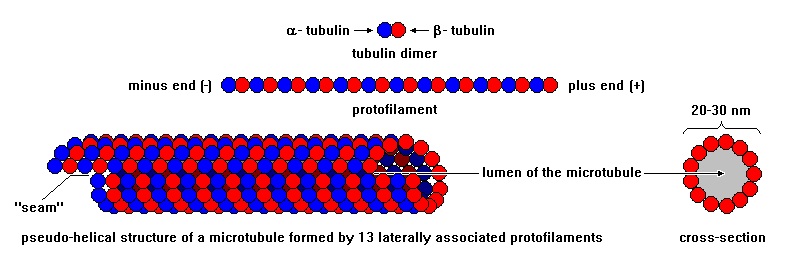
ここで「13」が出てくる原因として、私の昔の発表が掘り出されたようです:The Fibonacci sequence in nature implies thermodynamic maximum entropy(京都大学数理解析研究所講究録2013年)
こういうメールをアメリカの工業デザイナーの方からいただくことに、びっくりしました。
そこで、この発表を参照した論文等があるかを調べたところ、ひとつヒットしました。
「The Shannon Entropy of Fibonacci Numbers」
İhsan Tuğal、Bünyamin Şahi̇n、Abdulgani Şahin(2022.01)
MATI 4(1)(2022), 12-22
トルコの研究者のようです。発表した「http://www.matijournal.com」はもう消滅しているようです。
そのABSTRACTを読んでビックリしました。
Entropy is used as a tool to evaluate uncertainty of systems in the information sciences. Fibonacci number sequence is often appeared in the nature which is very related to golden ratio. Moreover, an early study shows that Fibonacci number sequence has maximum entropy in terms of thermodynamics in the nature. In this paper we compute the Shannon entropy of Fibonacci number sequence by the sum of these numbers. We obtain that the entropy measure is approached to 2,51179. In order to make some extra observations, we compute the Shannon entropy measures of odd indexed, even indexed Fibonacci numbers and the squares of Fibonacci numbers via the sum of these sequences. We obtain a very interesting result that the Shannon entropies of the mentioned sequences are approached to same value 1,55237.
ResearchGate:▶ ▶ ▶


そういうつもりはなく、あくまで仮説の提唱のつもりだったのですが、・・・これは責任重大ですね。
しょうがない、シャノンのエントロピーからクラウジウスのエントロピーも導き出そう。
ということで、このページを作りました。
やっつけ仕事になったのは、そういうことです。
最初はどうなることかと思いましたが、「絶対にシャノンンのエントロピーからクラウジウスのエントロピーを導き出せる」と確信をもって取り組みました。
なぜこれを10年前にできなかったのかというと、当時は教科書的なものに対して(つまり正統派の考え方に対して)遠慮しすぎていたのでしょう。
しかし、チラリチラリと、最近の YouTube とかを見てみると、「熱力学のエントロピー」=「情報のエントロピー」はもう常識になっているようにも感じられました。
もう10年近く何もしていなかったので、私は時代の変化に立ち残されたのでしょう。
情報エントロピーを使って熱エントロピーを導出するエレガントな方法はすでにあるのかもしれません(2025.12.20)。
エントロピーってよくわからないから、日常語として慣れ親しんでいる「エネルギー」を使って理解したいという方向けの説明です。
(2021年頃に作ったページであり)一部重複した説明が含まれますが、そのままにしておきます。
簡単に言うと、散逸構造とは、川の流れの途中に生じる渦模様のようなものです。

模様は別に渦巻でなくても構いません。何らかの水模様です。
そうした水模様を思い浮かべることができれば、次のことは容易に理解できると思います。


水模様に出入りする水の流れが妨げられると、最初にあった水模様は消えます。
では、水模様の中では何が起こっているのでしょうか?

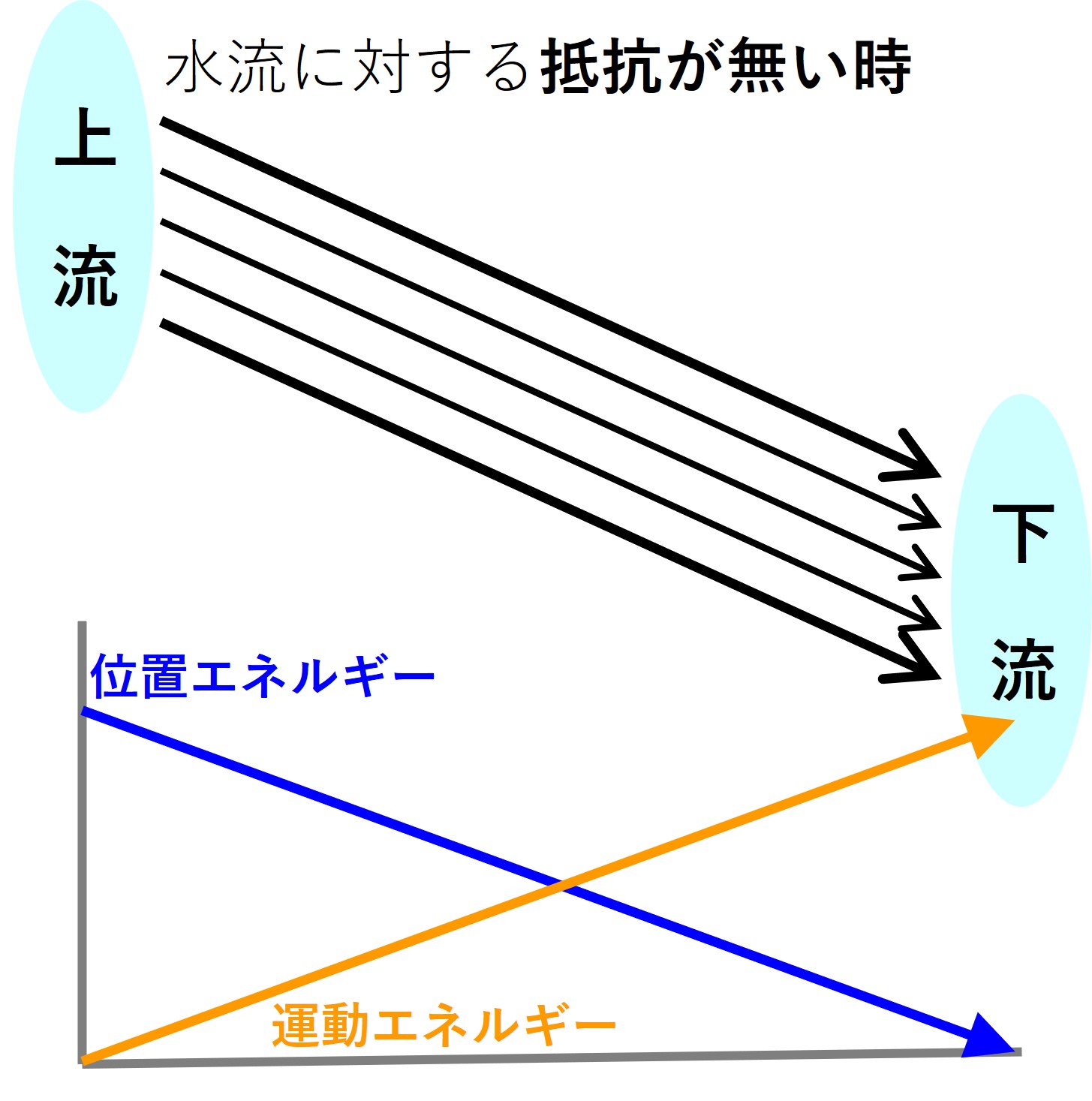
水の流れに抵抗が無い時は、水はサッーときれいに速く流れ落ちます。
上流で持っていた水の「位置エネルギー」は、すべて水の「運動エネルギー」に変わります。
位置エネルギー potential energy 、運動エネルギー kinetic energy って何という方は、振り子運動の図を見て思い出してください。
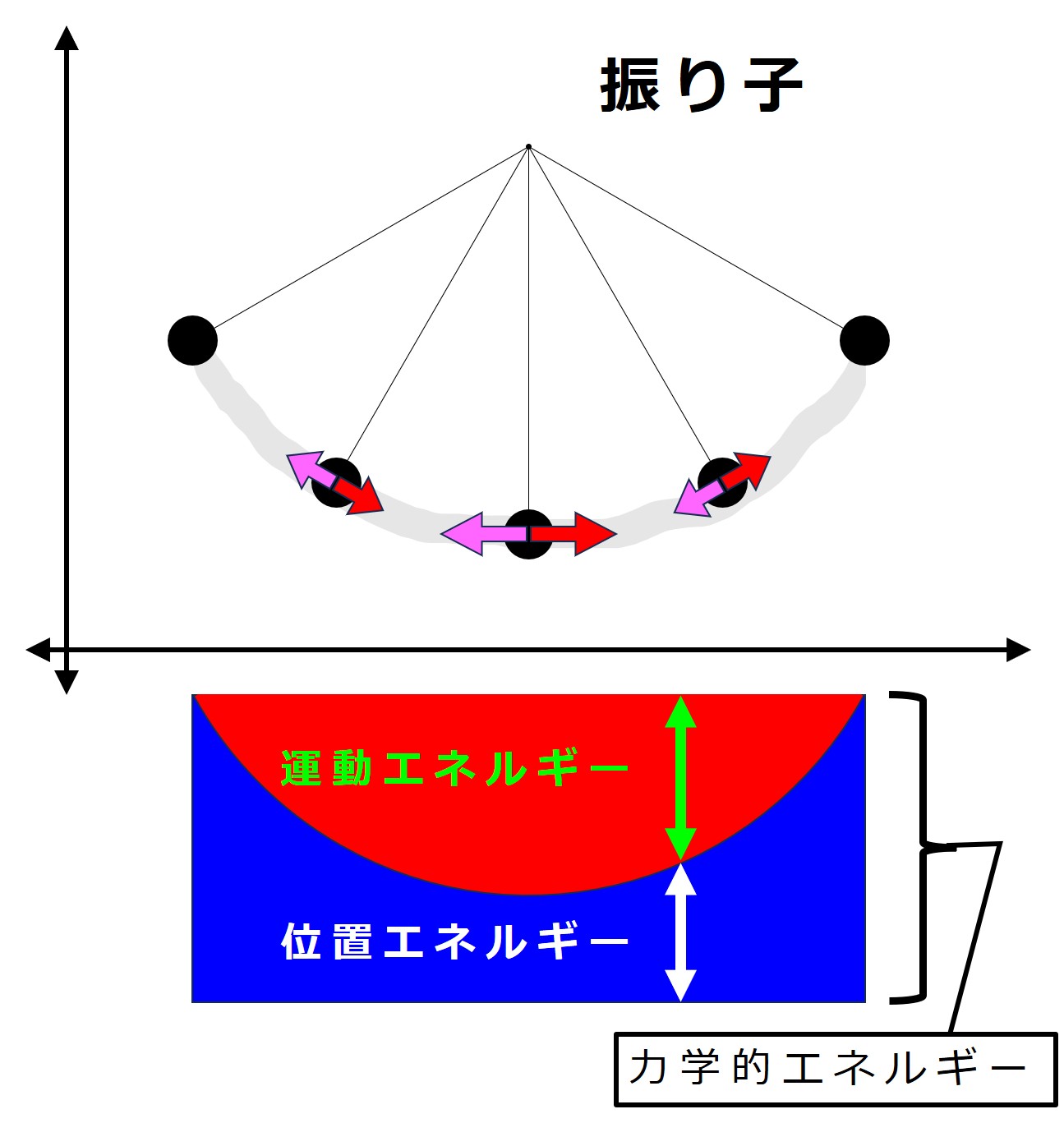
上流では下流に向かうほど、大きな高低差のために水の流れは速くなります。
滝を思い浮かべればよいでしょう。
下流へ向かう真っすぐな流れです。

しかし、水の流れに抵抗があると、水流と抵抗との摩擦(まさつ)により「下流へ向かう整った運動エネルギー」の一部は「複雑で乱れた運動エネルギー」に変わります。
このとき、水模様が造られます。
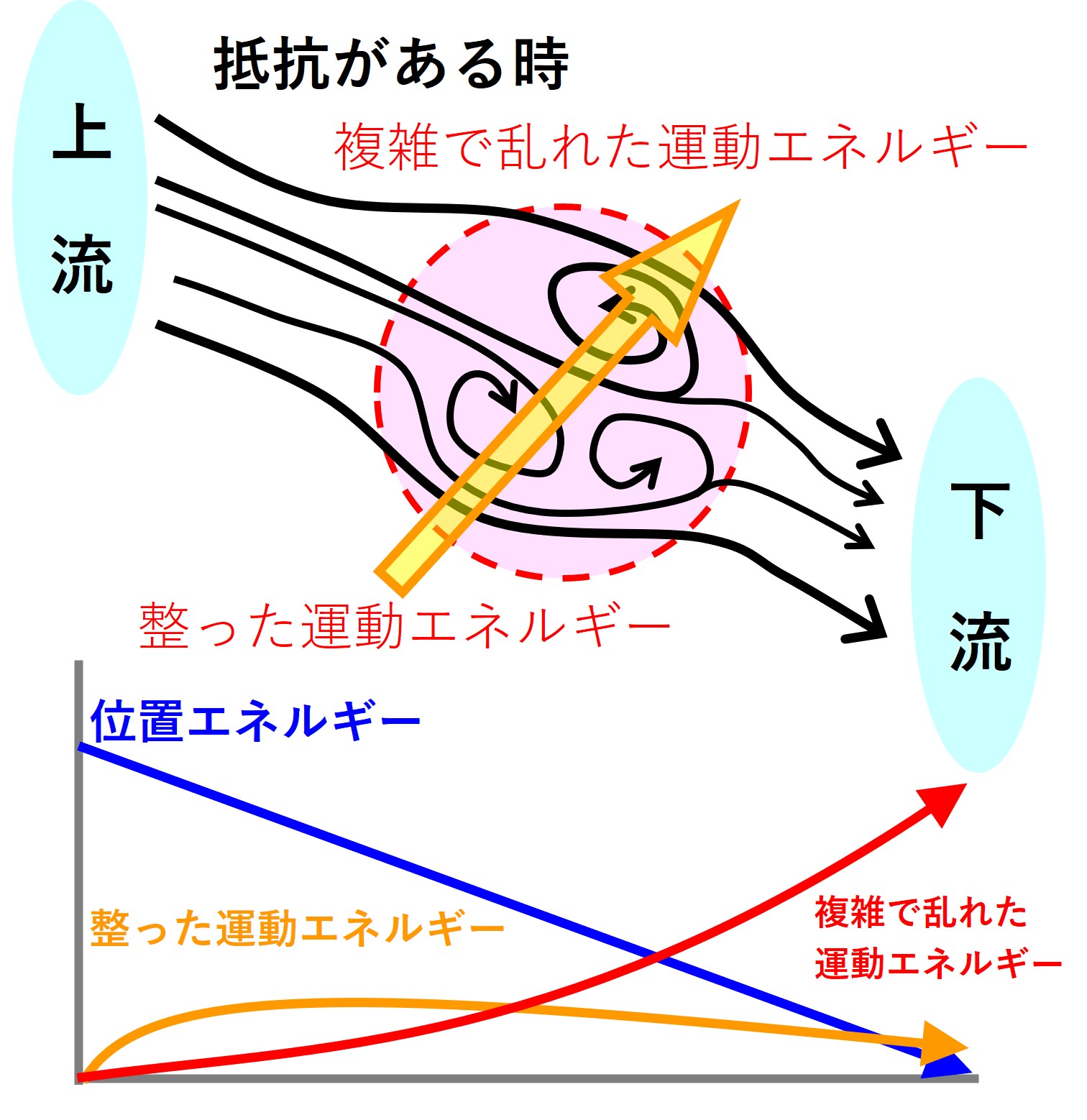
水模様は、言い換えると乱流です。
抵抗が無いときは、水はきれいに真っすぐ流れます(整流)。
抵抗との摩擦により流れが乱れます(乱流の形成)。
抵抗が大きいと乱れも大きくなります。
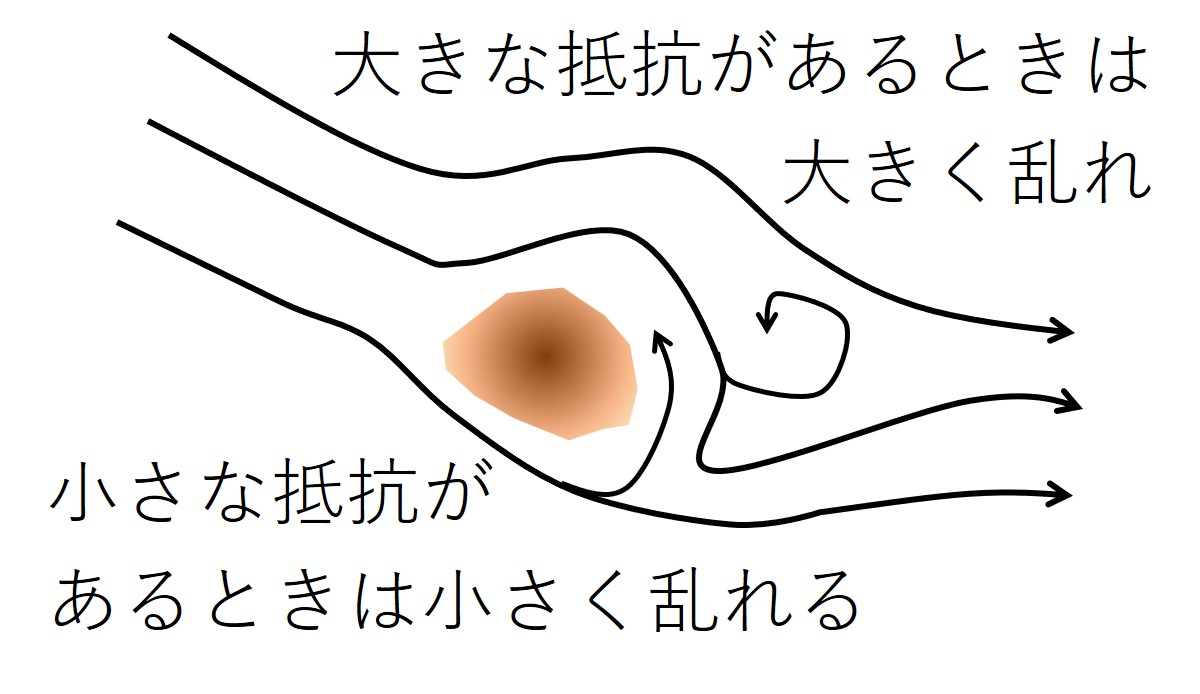
岸辺や川底にある大きな岩は大きな抵抗になります。砂利などは小さな抵抗になります。
しかし摩擦は、水流同士の間でも起こっています。
大きな抵抗で生じた大きな渦巻は、水流同士の摩擦により小さな乱れの集まりに散っていきます。
しかも、この変化は勝手に(自然に)進む変化です。
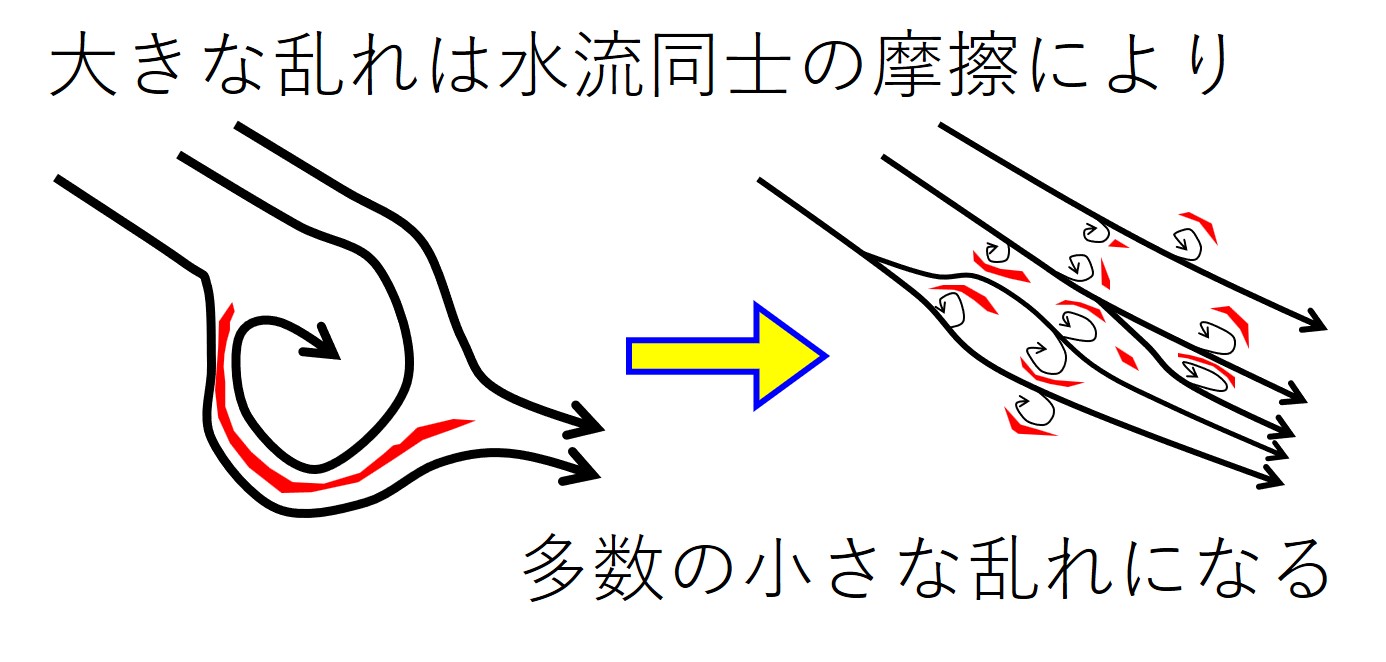
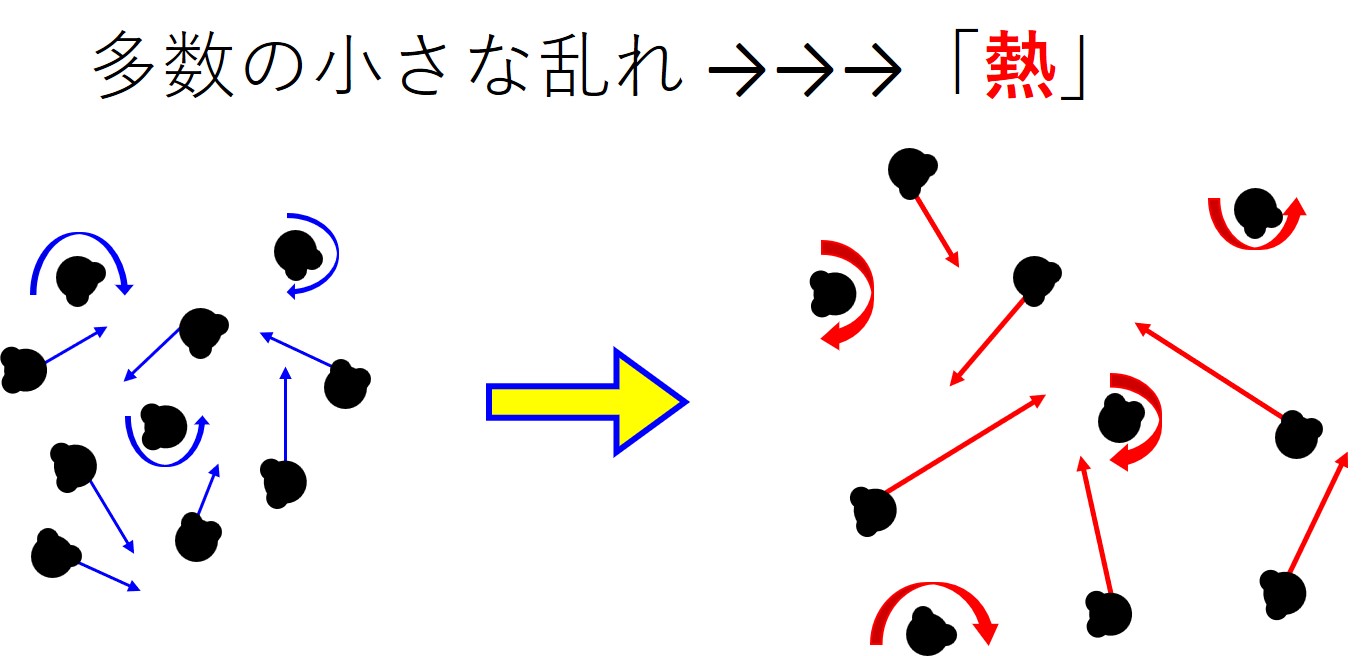
「乱れ」が、水流を構成する最小単位(水分子など)のレベルにまで分散したとき、それを「熱」として捉えることになります。
「複雑で乱れた運動エネルギー(乱雑な運動エネルギー)」は、比較的単純で肉眼で観察できるときは「水模様」として粗大な動きを見ることができますが、どんどん分散していくと究極的には「熱エネルギー」になります。

水模様の上流でも下流でも流速はほぼ同じだとすると、次の図のようになります。
高いところから低いところに水が流れると、高いところで持っていた位置エネルギーは「運動エネルギーの増加分」となりますが、それはすべて摩擦による熱エネルギーに変わります。
下流側の水温が上昇します。
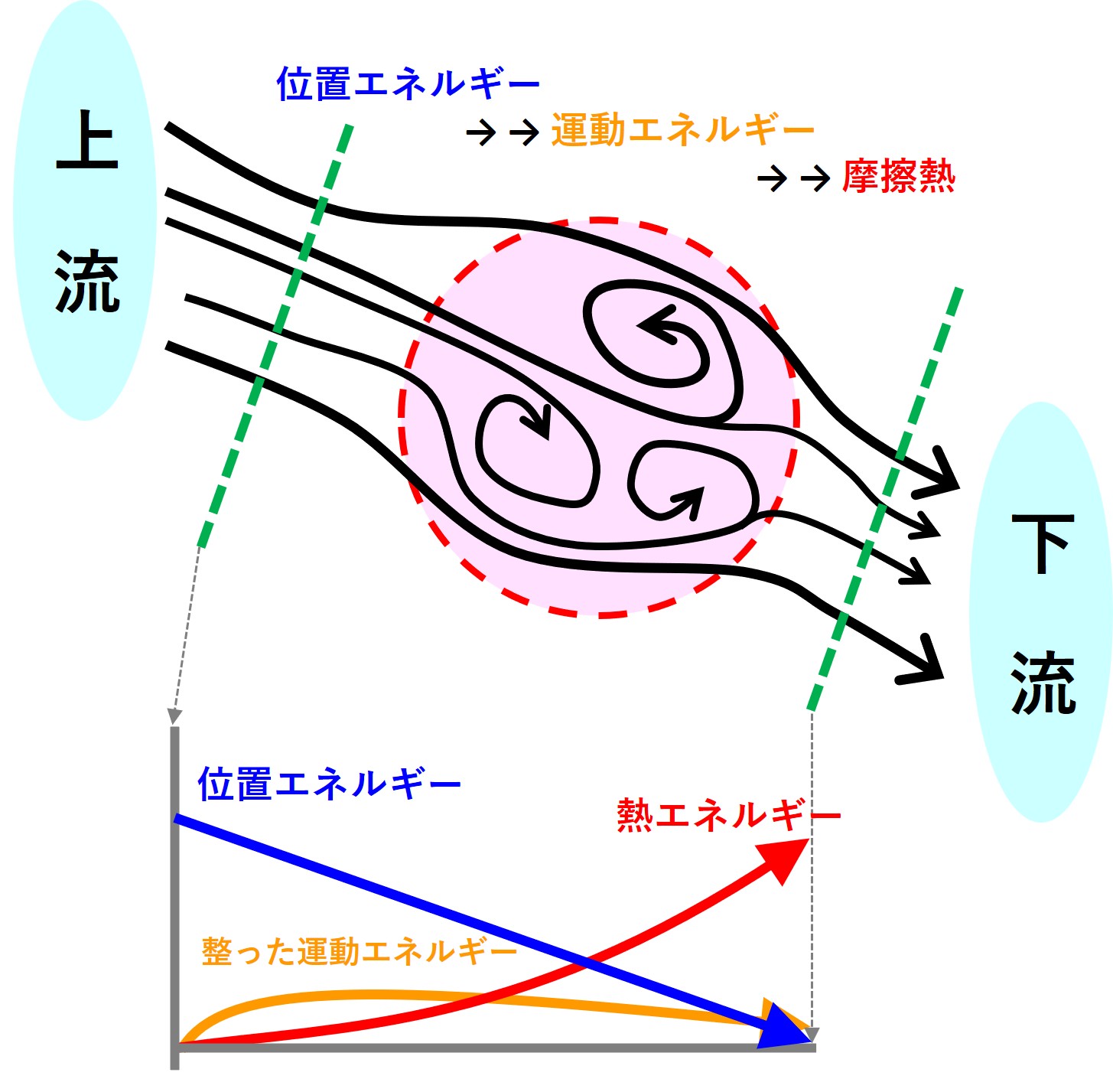
ところで、水流の総エネルギーは、どこでも一定です。これは「エネルギー保存の法則」です。
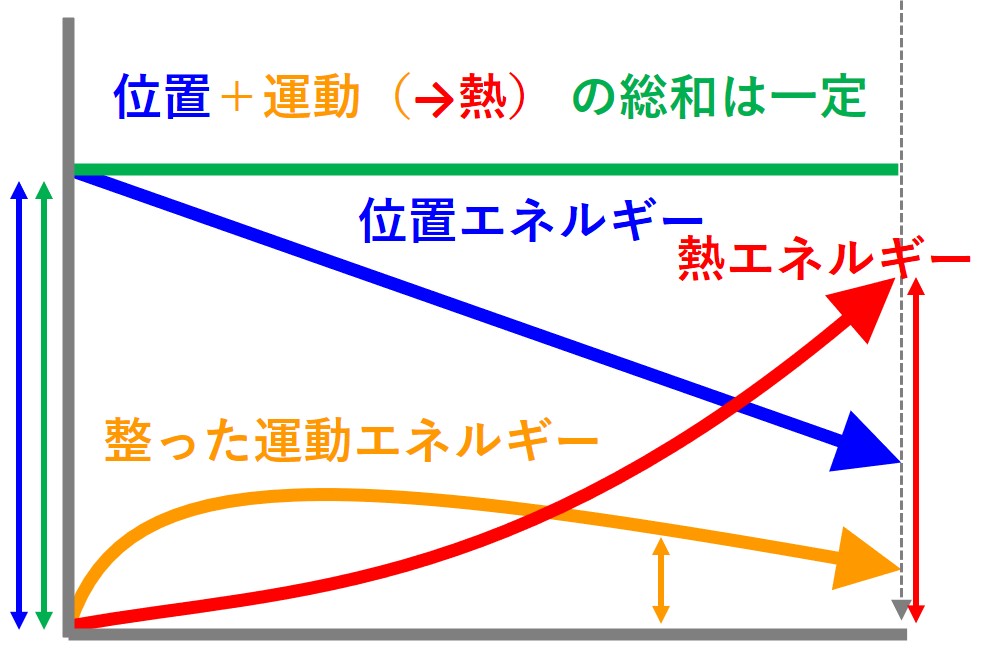
水模様の上流側も下流側も、エネルギーの量的な変化がないとすると、いったい何が変化しているのでしょうか。
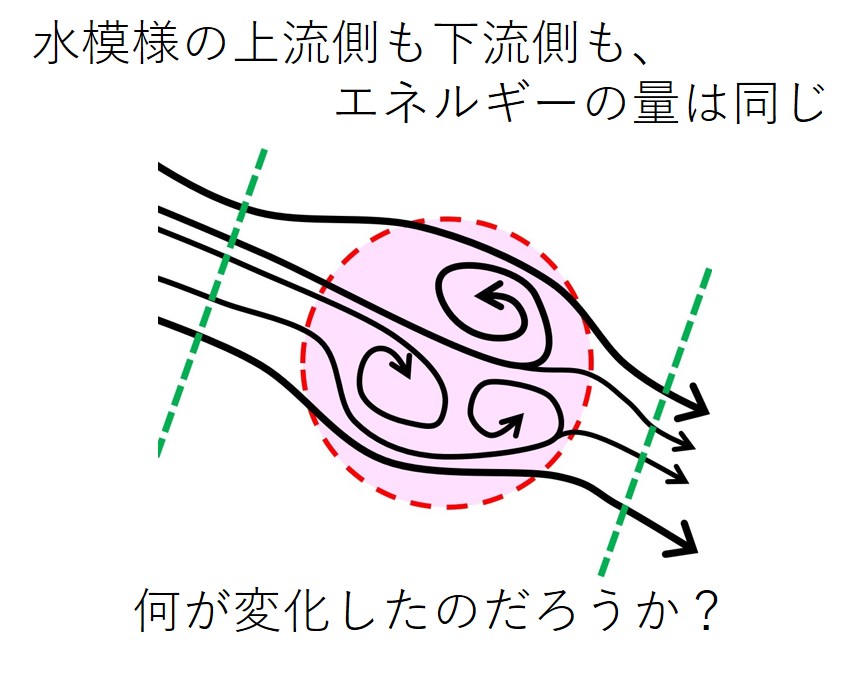
昔の科学者は、このような変化の 不可逆性 に着目しました。
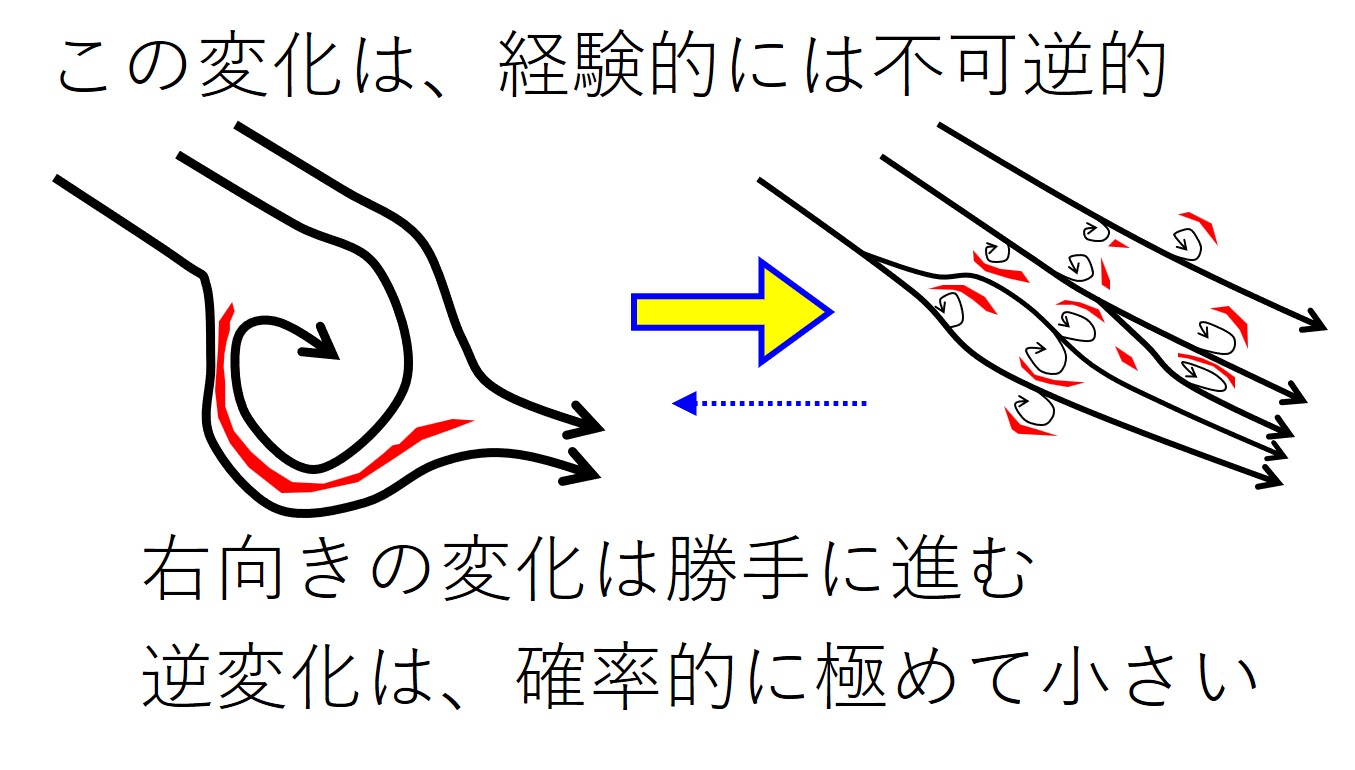
熱移動の不可逆性を研究したドイツの物理学者クラウジウス(1822-1888)は、乱雑な運動の程度を表す量として「エントロピー」を提案しました。
熱は、物体を構成する多数の粒子の複雑で乱雑な運動です。したがって熱エネルギーは「高エントロピーのエネルギー」です。
高い所から低い所に向かって水は流れます。
高い所で持っていた位置エネルギーは「低エントロピーのエネルギー」です。
流れ落ちる水の中で、「位置エネルギー → 運動エネルギー → わりと単純で粗雑な運動エネルギー(肉眼的な水模様) ⇒ 複雑で乱雑な運動エネルギー(熱)」と、高エントロピーのエネルギーに変化します。
上記の変化のうち、「→」は途中で止めることのできる変化ですが、「⇒」は自然に勝手に進む変化です。
特に孤立した系の中で、自然に勝手に一方向に(低エントロピー ⇒ 高エントロピー)進む変化の規則性を「熱力学第二法則」と呼びます。
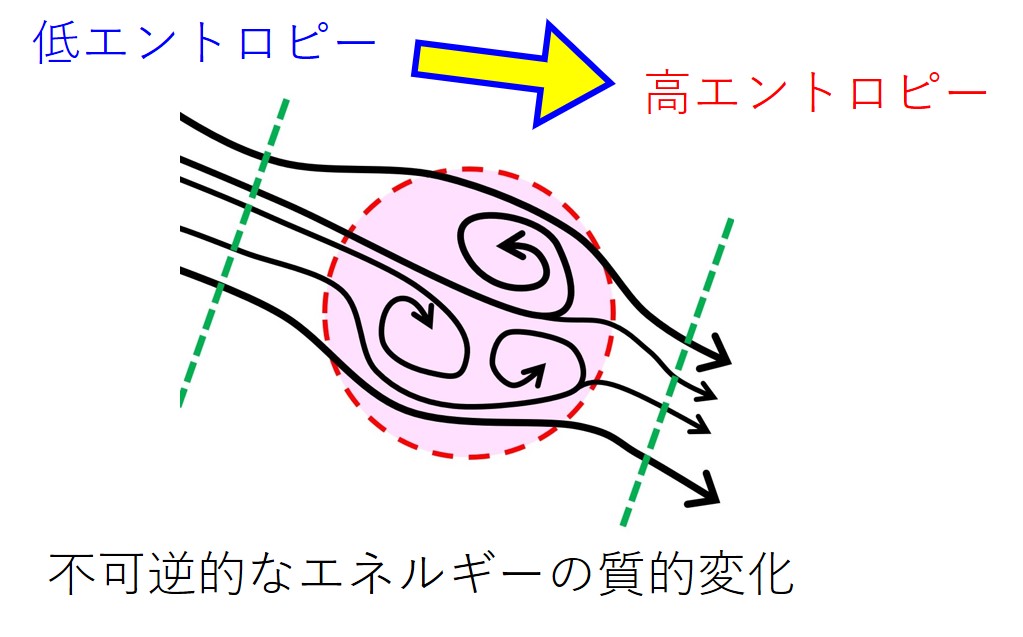
散逸構造とは、川の流れの途中に生じる渦模様のようなものです。
この渦模様が肉眼で観察できる「わりと単純で大きく粗雑な運動」に相当します。
この大きな渦巻の運動をずっと維持するためには、上流から水が常に流れ込むことが必要です(つまり、低エントロピーのエネルギーが構造の中に流れ込み続けることが必要です)。
また、この渦の内部では「多数の極微小な複雑で乱雑な運動」へ向かう変化が常に、勝手に起こっています。
この勝手に進む変化を放置していると、渦模様はすべて熱に変わってしまい、肉眼的な大きさの渦模様は消えます。
したがって、この渦模様が長時間保たれるためには、内部で発生し続けている「熱(多数の極微小な複雑で乱雑な運動)」を渦模様の外に、絶えず捨て続ける必要があります。
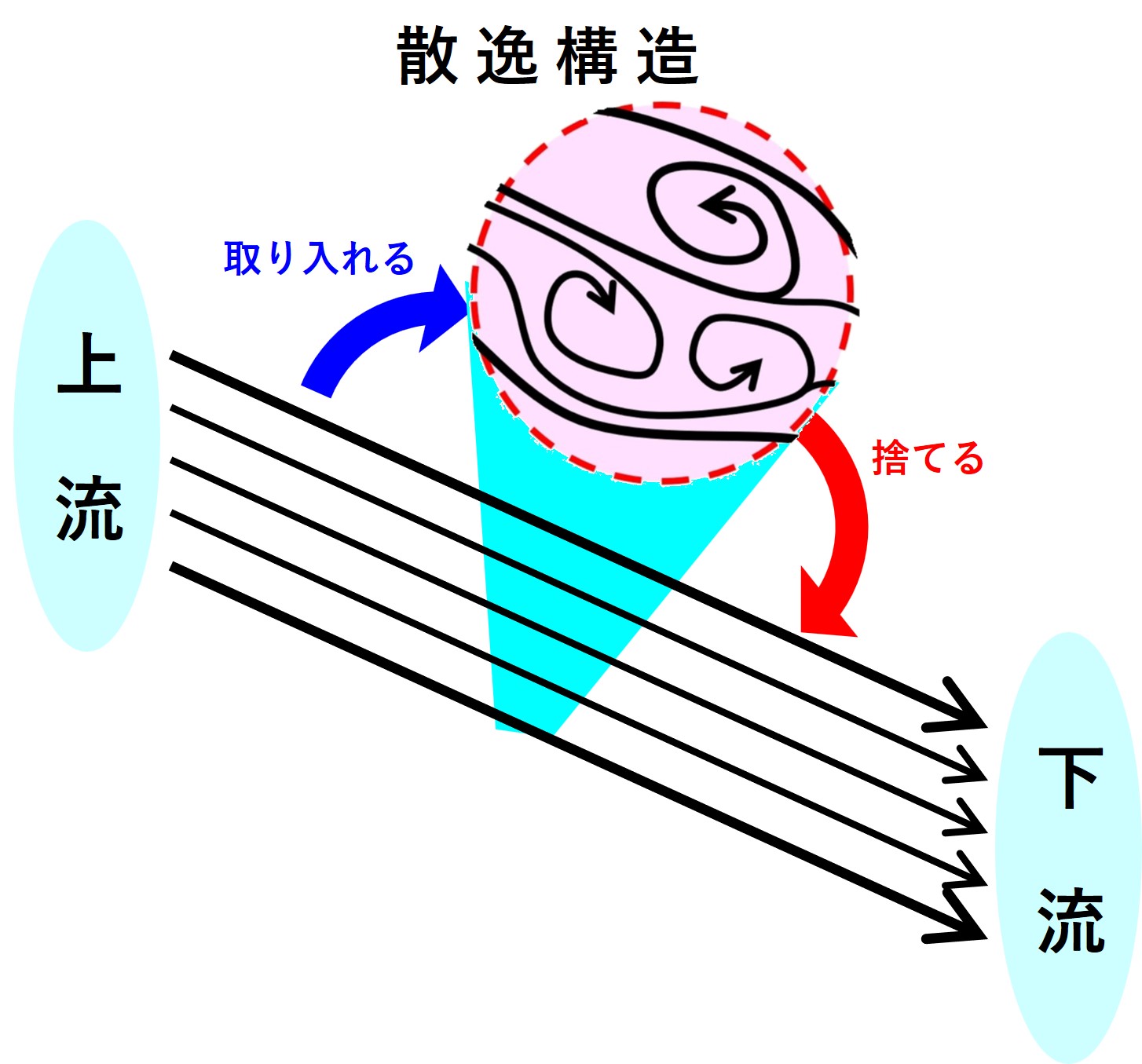
低エントロピーのエネルギーが流れるときの摩擦により「単純で粗大で乱雑な運動(散逸構造)」が生じます。
散逸構造の中では、勝手に「多数の極微小で乱雑な運動(熱)」への変化が進み、肉眼的に認められた構造は消えていきます。
この散逸構造が維持されるためには、「低エントロピーのエネルギー流入が保たれること」と「内部で発生した熱(高エントロピーのエネルギー)が外部に捨て続けられること」とが必要です。
この「流入する低エントロピーのエネルギー」と「高エントロピーのエネルギー」とのバランスで、散逸構造は維持されます(成長したり、消退したりします)。
では、具体的な例で見ていきましょう。
散逸構造の例をあげます。
最初の例は動物です。動物は散逸構造です。
食べる食料や呼吸で取り入れる空気が低エントロピーのエネルギーです。飲んだり食べたりする物や空気の平均温度は体温よりも低くなくてはなりません。
食べ物は消化され、栄養を吸収されてウンチ💩になります。
ウンチの構造を思い描いてください。あらゆるものが混じり合って乱雑ですね。ウンチは高エントロピーのエネルギーです。
体内では新陳代謝が進み、熱が産生され続けます。
動物の体表からは水分が蒸発しています。その気化熱により身体は冷えます。
上流を断っても、下流を断っても、動物は死にます。
同じように植物も散逸構造です。
植物が取り入れるのは太陽からの光エネルギーです。光は高品質の低エントロピーエネルギーです。
光エネルギーは植物によって有機分子の化学的な結合エネルギーに変わります。動物は植物を食べて低エントロピーのエネルギーを得ます。
細菌も散逸構造です。
すべての生物は散逸構造です。
散逸構造の特徴は、エネルギーの流れの上流あるいは下流が断たれることにより命絶える(構造が消滅する)ことです。
「寿命」があるものはすべて散逸構造です。
都市は散逸構造です。廃墟になりますね。
国家は散逸構造です。滅亡しますね。
現代文明も散逸構造です。いつかは消滅します。
宗教も散逸構造です。信者がいなくなれば消滅します。
イリヤ・プリゴジンというベルギーの科学者が1977年、散逸構造論でノーベル化学賞を受賞しました。
このとき、欧州のキリスト教の偉い指導者は、「散逸構造論をあらゆる現象に敷衍(ふえん)すべきではない」と警告したそうです。
散逸構造論ではどんな宗教も相対化されてしまいます。その危機感があったのでしょう。
生物は散逸構造であり、生物についてのダーウィンの進化論はあらゆる散逸構造に適用できます。
生物以外にも拡大した進化論を「一般進化論」と私は呼んでいます。
一般進化論は、実は仏教のエッセンスそのものです。日本人にはとても馴染みのある考え方です。
「平家物語」の世界観は、仏教の無常観です。鴨長明の「方丈記」で描かれているのも散逸構造です。「第2説明」で紹介しています。
少し難しいとは思われますが、日本はどうして米国と戦争しても勝てないのかを一般進化論の立場から論じたものを紹介します。
◆ 「創造的作戦の起源」(2008.07.30) PDF:▶ ▶ ▶ MS Word:▶ ▶ ▶
エントロピーとは何か。
エントロピーを作るもと(元、素)は「確率」です。
では、確率とは何か。
小学校の頃から教わり、なんとなくわかっているつもりの確率を実際にはよく理解できていないので、エントロピーのことがよくわからないのかもしれません。
モンティ・ホール問題において示される人間の直観的な確率感は、量子力学的な根拠を持っているのだろうという仮説に基づいてミクロレベルで確率の正体に挑戦し始めています。
エントロピーの理解を阻む「確率」の壁を突破することが重要なのだろうと考えられます。幾多の失敗を求めて、思索の暴走を続けましょう:▶ ▶ ▶
Home:▶ ▶ ▶